图形学杂记（光栅化）

简介

这是一个图形学杂记，从光栅化到RT的诸多东西都乱记在里面，大多数只在这里记录了基本思想（有些暂时理解不深的也简记在这里），具体的一些东西可能会另开一贴来记录。

投影

“投影”直观上容易被理解为将三维空间物体变换到二维屏幕的过程（可以有这样一种降维的线性变换），但如果直接用矩阵来做这样一件事，不方便处理深度信息（遮挡效果）。

故实际上我们说的投影矩阵，是将三维空间中的一个长方体或平头截体（观察区域）映射到标准立方体（Canonical Cube，$[-1, 1]^3$）的过程，这个空间也叫裁剪空间。映射到这里的好处是方便进行后续操作。

正交投影

将一个长方体映射到 $[-1,1]^3$，比较简单

很多时候我们会在正交投影时把 $z$ 倒过来，这样摄像机朝 $-z$ 方向，而深度缓冲中的 $z$ 越小表示离摄像机越近。

透视投影

透视投影的观察区域是一个平头截体，我们希望也使用一种（四维矩阵可表示的）线性变换将它映射到 $[-1,1]^3$。

思路：首先进行的是一个“压扁”的缩放过程，令远处的平面缩放幅度更大，近平面不变，使得平头截体变成一个长方体，随后进行正交投影。

最简单的想法：让一条观察射线（朝-z方向）上所有 $x,y$ 坐标缩放后都相同，先假定 $z$ 轴不变。

通过相似三角形容易计算出新坐标应该为 $(n/z\times x,n/z\times y,z)$

编出一个变换矩阵，其中参数 $n$ 为近平面的 $z$ 坐标（负值！）
$$
\begin{bmatrix}
n&0&0&0\
0&n&0&0\
?&?&?&?\
0&0&1&0\
\end{bmatrix}
\times
\begin{bmatrix}
x\
y\
z\
1\
\end{bmatrix}
=
\begin{bmatrix}
n/z\times x\
n/z\times y\
z\
1\
\end{bmatrix}
\rightarrow
\begin{bmatrix}
nx\
ny\
z^2\
z\
\end{bmatrix}
$$

我们发现1，2，4行的参数都很容易确定，但是第三行似乎没法搞？

问题出现了，这样的变换似乎不是一个线性变换（即使在四维下）

那么只能放弃追求 $z$ 轴不变了。

实际的投影矩阵要求只有：近平面坐标不变，以及远平面的z轴（$f$）不变

$$
\begin{bmatrix}
n&0&0&0\
0&n&0&0\
0&0&A&B\
0&0&1&0\
\end{bmatrix}
\times
\begin{bmatrix}
x\
y\
n\
1\
\end{bmatrix}
=
\begin{bmatrix}
nx\
ny\
n^2\
n\
\end{bmatrix}
$$

$$
\begin{bmatrix}
n&0&0&0\
0&n&0&0\
0&0&A&B\
0&0&1&0\
\end{bmatrix}
\times
\begin{bmatrix}
x\
y\
f\
1\
\end{bmatrix}
=
\begin{bmatrix}
nx\
ny\
f^2\
f\
\end{bmatrix}
$$
$$
An+B=n^2\
Af+B=f^2\
A = n + f\
B = -nf
$$

由此得到了这个压缩矩阵：
$$
\begin{bmatrix}
n&0&0&0\
0&n&0&0\
0&0&n+f&-nf\
0&0&1&0\
\end{bmatrix}
$$

现在得到需要的矩阵了，它满足变换后近平面不变，远平面 $z$ 不变，且中间的 $z$ 坐标依旧保持顺序的性质，变换到 $[-1,1]^3$ 之后大概长这样：

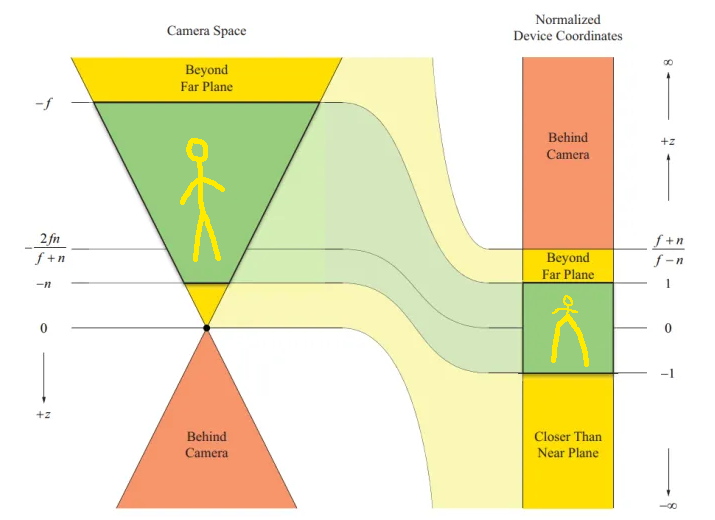
（图源网络且魔改）

可以看到，虽然它让中间部分保持了顺序，深度测试不会出错，但是不均匀地拉伸会让三角形内部的插值有很大问题，需要进行下一节所说的透视插值矫正。

但这样的不均匀也不是没有好处：它将深度测试中我们所说的“非均匀精度分配”直接实现了！

LearnOpenGL：

可以看到，深度值很大一部分是由很小的z值所决定的，这给了近处的物体很大的深度精度。这个（从观察者的视角）变换z值的方程是嵌入在投影矩阵中的，所以当我们想将一个顶点坐标从观察空间至裁剪空间的时候这个非线性方程就被应用了。

再次体会到投影矩阵的强大

手动推导一下这个深度变换式子：

“压扁”后：$z_1 = n+f-nf/z$

标准坐标系内：$z_2=-1+2\times (n-z_1)/(n-f)$

如果深度值范围是0-1：$z_3 = (z_2+1)/2 = (n-z_1) / (n - f) = \frac{(1/z-1/n)}{(1/f-1/n)}$

和LearnOpenGL上给出的式子完全一致！简洁优雅

透视插值矫正

图不想画了，二维情况下的计算不难，推广到三维也很合理，直接给出结论：

设屏幕空间下，某点的重心坐标为 $a,b,c$，则该点的实际深度值 $w_0$
$$
\frac{1}{w_0}=\frac{a}{w_1}+\frac{b}{w_2}+\frac{c}{w_3}
$$
插值结果（假设对 $p$ 这个属性插值）：
$$
p_0 = w_0\times(\frac{ap_1}{w_1}+\frac{bp_2}{w_2}+\frac{cp_3}{w_3})
$$
推导链接

注意：这里用 $w$ 表示顶点在透视投影变换前的 $z$ 坐标，为顶点的实际深度，要和变换到标准设备坐标下之后的 $z$ 坐标作区分。

这个 $w_{123}$ 是怎么留下来的呢？还记得投影矩阵变换后的 $w$ 分量吗，它恰恰等于原先的 $z$。我们通常会在齐次除法中保留它不变（因为后面也不会用到线性变换了，留着也没关系（视口变换可以直接操作）。

最后，深度测试使用的深度值并不是 $w$（如果用 $w$ 就做不到非均匀分配精度了），而是NDC下的 $z$ 坐标。我们可以用三个顶点的 $z$ 坐标按照上述方式插值到单点的 $z$ 坐标，它早在投影时便完成了精度的分配。

反走样

可以采用先模糊，再采样的方法。

理解走样的来源是：采样频率跟不上信号变化的速率，两个采样点之间信号可能发生了很多未被采集到的变化。

模糊操作本身是对信号做了一个均值处理，此时一个像素上包含了其附近像素的信息，故模糊后采样能非常有效地缓解锯齿。

另一个角度：模糊操作相当于一个低通滤波，除去了高频部分。而锯齿现象本质是源于对高频信号采样时的信息缺失。

从这两个角度都可以理解：为什么先采样，后模糊不行。

模糊的一种办法是对连续图像取平均得到离散结果。具体到三角形上，可以在每个像素处根据覆盖三角形的面积来改变颜色，再具体的，可以在每个像素中设多个采样点（4个，9个..），看几个在三角形内来粗略计算面积（MSAA方法）。

着色

• Flat Shading，逐三角形着色，每个三角形的法线都完全一样，适用于有锐利转折的平面。

• Gouraud Shading，逐顶点着色，在顶点处计算出颜色，将颜色/光强插值到各个片元。

  • 双线性光强插值指的也是这个

• Phong Shading，逐像素着色，将顶点法线插值到像素上后逐像素计算颜色。效果最平滑，也比较常用。

  • 双线性法向插值指的也是这个

顶点法向量：近似地由各个相邻面的法向量平均得出。

具体插值方法

重心坐标

重心坐标（Barycentric Coordinates）定理：即三角形中任意一点 $X$，都可以表示成 $X=aA+bB+cC$，其中 $ABC$ 为三个顶点的坐标向量，$abc$ 为系数且满足 $a+b+c=1$。

一个顶点的重心坐标可以用这样的 $(a,b,c)$ 来表示，实际上，可以根据顶点对面的三角形面积占比来快速计算 $abc$（具体图去百度找一下）

重心坐标本身就代表了三个顶点在此点所占的权重，故可以轻松得到插值比例。

双线性插值

具体思路：先插值一次得到每条线上的值，再插值得到每个位置上的值。

可以利用扫描线算法，进行增量插值。

图像放大方法

高分辨率对象上应用低分辨率图像时常用算法：

• Nearest：取最近像素
• Linear：线性插值，按距离分配权重，取周边像素均值
  • BiLinear：对于图像而言的双线性插值，按水平和垂直线性插值两趟
• Bicubic：双三次插值，效果更好，原理涉及信号系统（暂略）

图像缩小方法

低分辨率对象上应用高分辨率图像（渲染远处物体上常见这种情况），一个屏幕像素对应了多个纹理像素，采样时理应取均值。

但按原本的采样方式，会仅取到中心处的纹理像素，它显然无法代表这一片区域的像素值。也就是说我们需要进行区间查询操作，实际进行的是单点查询。

于是有了mipmap（多级渐远纹理），其本质是预处理的思路，有点类似线段树。

Mipmap

即对于一张纹理，事先将其缩放为一半、1/4、1/8…（缩放时计算了区间均值），将这些缩小的纹理全都存放起来。这些全部存放的空间仅为原先的 $4/3$ 倍。

具体渲染时，对于一个即将渲染的像素（已经知道了其uv），可根据它与相邻像素uv的差值，估算出它覆盖了多大的纹理（pixel footprint）。

注意这是一种粗略的近似，像素实际覆盖的纹理区域不一定是矩形，而mipmap方法根本上是对一个矩形区域求了均值，故这里并不完全准确。

假设现在这个像素需要覆盖一个宽为 $L$ （个纹理像素）的正方形，那么实际如何利用多级渐远纹理取样？

• Trilinear：三线性插值，计算 $D=log_2 L$，即要在第 $D$ 层纹理上取样比较合理，$D$ 为浮点数时就，在 $\lfloor D\rfloor$ 和 $\lfloor D\rfloor +1$ 层分别进行双线性插值，然后再依据 $D$ 插值一次得到实际颜色。

Ray differential

上述计算footprint的方式只在光栅化框架中可行，在路径追踪中，我们需要追踪纹理uv对屏幕像素xy的偏导，如 $\frac{\partial u}{\partial x}$，即屏幕像素偏移1单位时，uv偏移了多少，它可以用于估计pixel footprint。

具体而言，我们可以记录当前光线对屏幕像素的偏导 $\frac{\partial \bold R}{ \partial xy}$，其中 $\bold R = \vec O + t\vec D$，在光线传播过程中分别维护 $\frac{\partial \vec O}{\partial x}$，$\frac{\partial \vec D}{\partial x}$….等等信息。

具体更新方式可查原论文，在大多渲染器框架中此功能都已经实现。

各向异性过滤

Mipmap只能求正方形区域的均值，故在覆盖斜着的、长的纹理时会出现overblur（过度模糊）的现象。

各向异性过滤额外预处理了一些不等比缩放的纹理（具体图百度），空间翻到了3倍，能很好地处理覆盖区域为长方形的情况，但对于斜长的情况还是会overblur。

EWA filtering是一种更复杂的方法，具体略过。

纹理应用

环境贴图

可以用来做天空盒、环境光等全景贴图。

一种方式是使用六个张纹理做立方体贴图，另一种方式是使用球面的展开图。

两种方式都能用三维向量来采样纹理，球面展开方式是将球面坐标作为展开图的xy坐标。

通常，将矩形贴图转换到球面坐标的环绕方式是这样的：

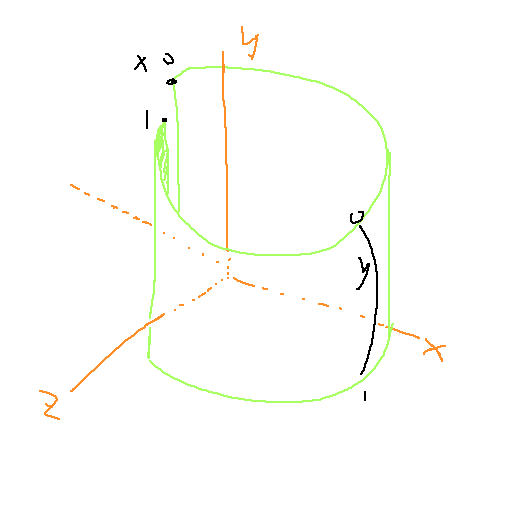
法线贴图

字面意思很好理解，用纹理来直接指定每一个像素上的法线，能在平面上做到丰富的光照细节。

但直接在模型空间下指定法线，不是太好。例如当一个立方体的六个面都使用相同的纹理时，我们却不得不为它分配六张不同的法线贴图。

一个更好的坐标系是切线空间，在切线空间下表示法线，可以只关注平面，而不关心其方向。

切线空间

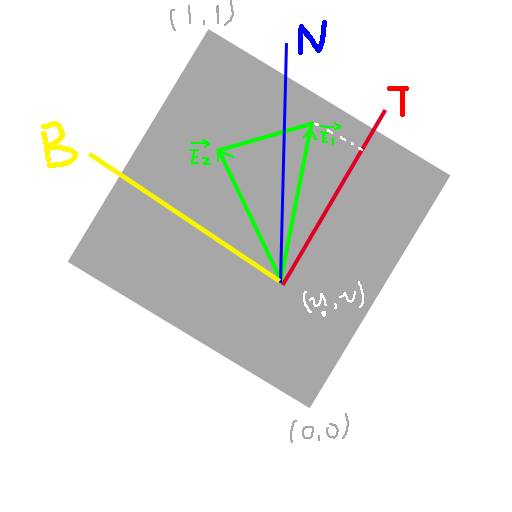
对于一个表面而言，法线是唯一的，而切线可能有很多种，通常会将uv展开的方向定义为切线。

具体如图所示，绿色为空间中任一个三角形，灰色部分为将这个三角形的纹理（uv）直接贴上去的样子，我们定义沿纹理 $x$ 轴方向的单位向量为切线 $T$（Tangent），同时沿纹理 $y$ 轴方向的单位向量为 $B$（bitangent），三角形的法线朝向 $+z$ 方向，这样的空间叫做切线空间。

切线 $T$ 通常作为顶点数据的一部分，会在模型中给定，如果希望自己算，也可以通过上图中三角形的另外两点的顶点坐标和uv列式计算得到。

具体式子可以来这边找到 https://learnopengl.com/Advanced-Lighting/Normal-Mapping

使用切线空间来应用法线贴图的流程大概是这样的：

• 将 Normal、Tangent 以及MVP这类的矩阵传入顶点着色器，也可以预先将法线矩阵（3x3的逆的转置的那个）计算好传入。
• 叉乘得到 Bitangent，将三个轴都变换到世界坐标系下（同法线变换方法），得到 TBN 矩阵
• 把 TBN 矩阵传入片段着色器
• 在片段着色器中，从 Normal map 中采样法线，然后让这个法线左乘 TBN 矩阵即可得到世界坐标系下的法线。
  • TBN是一个仅有旋转的3x3矩阵，故不需要再进行法线变换。

如果在观察坐标系下计算光照，也是同理。

我们通常看到的法线贴图偏蓝色，正是因为切线空间下法线大多朝向 $+z$ 方向（0, 0, 1），仅对一部分细节有所扰动。

在多个三角面共享顶点时，我们用类似法线的处理思路：如果希望有平滑的效果，就平均一下，如果要锐利就把公共顶点拆开。

细节

normal map会导致某些角度的入射/出射光，在宏观表面的上方，但却在normal所示的表面下方（反之一样），这种情况下进行光照计算会有歧义。

参照mitsuba中的法线贴图实现，若光源方向遇到了这种情况，直接舍弃；而若观察方向遇到这种情况，不舍弃，按照normal所示的新表面计算（可能由反射变成透射）

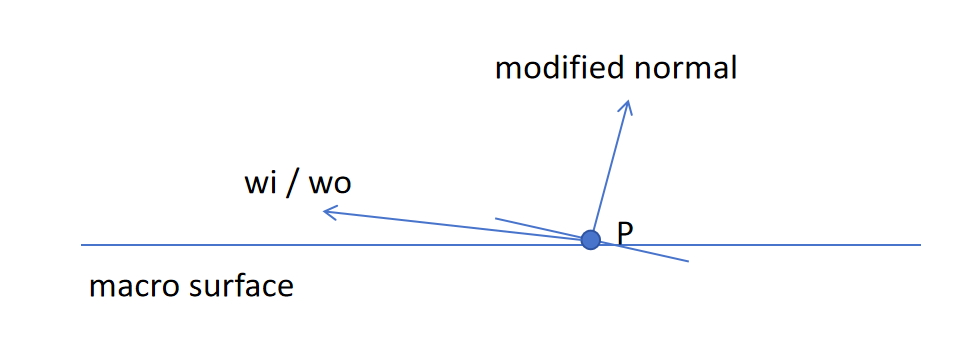
这个地方究竟应该如何舍弃，目前我还没找到什么逻辑严谨的定论，暂且按照mitsuba来。

upd: 最新发现，这个特性通常在几何项中被处理（包括mitsuba中），也即两个方向都会产生这样的遮挡。

凹凸贴图

更直观的做法：不是直接指定每个像素的法线，而是指定每个像素的高度偏移，然后自行计算法线。

计算法线同样在切线空间下进行，假设原法线朝向 $(0, 0, 1)$，可以在凹凸贴图上做个差分来计算新法线。
$$
dp/du=c_1\times (h(u+1)-h(u))\
dp/dv = c_2\times (h(v+1)-h(v))\
n=(-dp/du,-dp/dv,1)
$$

阴影贴图

实现阴影的经典办法，但是有非常多弊端。

思路：首先在光源位置观察场景，走一遍光栅化流程（但不着色），渲染出一张阴影贴图，每个像素上记录深度。

然后再正常渲染场景，对于每个片段，我们再将这个片段变换到光源的观察坐标系下，做一次投影，找出这个片段在阴影贴图上对应的位置。然后对比深度值，以判断这个像素是否能被光源看到。

上述是最简单的阴影贴图逻辑，它只能处理平行光，只考虑了单光源，只能产生硬阴影，且依赖阴影贴图的分别率，容易产生锯齿。

多光源

本身我们在着色时，多光源就是分别着色后叠加的。因此阴影只对每个光源分开考虑就好。

软阴影

麻烦 跳过

HDR与色调映射

HDR High Dynamic Range 高动态范围，指使用不限制的范围（超过 $[0,1.0]$）来表达场景亮度，在需要显示时（显示器只能显示 $[0,1.0]$ 之间的亮度）再转换到低动态范围 LDR。转换的方式叫色调映射（Tonemapping），一般不是简单的线性转换，而是通过特殊手段尽可能保留场景细节。

Reinhard色调映射

$f(x) = \frac{1}{x+1}$

简单好用，偏向亮色

Gamma矫正

物理亮度是正比于能量（光子数量）的，人眼看到的感知亮度实际为 $物理亮度^{1/gamma}$

如果我们不进行任何处理，图片直接按物理亮度存储，显示器按物理亮度发射光线，我们人眼看到的颜色也是对的（和拍摄时的颜色相同）；但这样，图片的存储密度对于物理亮度而言是均匀的，但对于感知亮度就不均匀了。

对于人眼而言，信息利用率没有做到最好，直观的感受就是，调颜色会发现颜色的变化不均匀。

因此，现在绝大多数电脑图片都存储在sRGB空间下，也即按感知亮度存储。

对于大多数使用者，不需要关注到gamma矫正的存在，因为他们始终在感知亮度空间下工作。而我们在进行光照运算时，必须转换到物理空间下进行。

通常说的线性工作流，指的就是在物理空间下进行计算，线性空间通常指物理亮度空间。

常用到的一些知识：

• 大多数图片（ jpg, png 等）都存储在sRGB空间，线性工作流中应将他们变换到物理空间进行运算；exr 文件存储在物理空间，不需要转换。
• 在线性空间下计算的渲染结果若要保存为 jpg, png 等，应将输出颜色变换到感知空间。我们只需负责按sRGB格式保存正确的图像，显示器会自动完成sRGB的显示工作（变换到物理空间去决定发射多少光子）。
• 美术工具通常都是工作在sRGB上的，各种调色板调的通常都是sRGB。专业的显示器和软件（tev等）一定会考虑到线性空间和sRGB的不同，进行显示、格式转换时都会进行Gamma处理。
• OpenCV 在读取图像时并不会进行处理，很多CV工作都是在LDR、感知空间下计算Loss的，这也合理，这样计算的Loss更符合人眼感受。需要注意的是如果我们要使用别人预训练的网络，最好也先将HDR值截断，再将图像转换为sRGB输入。
  • 这里我们说到截断。事实上在科研中Tone mapping大多数时候是不用的，它更多是一个游戏或者显示器中的功能，用于提升画面细节。我们也不希望读取图像时还要进行反向Tone mapping。
  • 最近发现做CVCG科研的人好像都认为Gamma矫正也是一种Tone mapping，这个在CG的线性工作流中就是必须的了。

Sobol序列

Sobol序列是一种低差异序列，支持生成大量的 $n$ 维点集。我们用 $x_{i,j}$ 表示第 $i$ 个样本的第 $j$ 维。

其每一个维度 $j$ 需要一个二进制生成矩阵 $C_j$（有了生成矩阵后，Sobol可以通过index $i$ 计算出第 $i$ 个数，计算过程很多地方都有，此处不赘述）

为了方便，通常会使用32x32或64x64的生成矩阵，这样可以将一行/列视为一个二进制表示，用一个整数存储。因此生成矩阵通常显示为一串整数。以32x32的生成矩阵为例，它可以支持 $2^{32}$ 个样本。当然，这并不是Sobol的理论上限，理论上只要我们愿意去实现更高维的生成矩阵，它支持的样本数量是无限的。

Sobol官网 给出了一些文件，这里重点讲一下这个文件的用法：

d       s       a       m_i     
2       1       0       1 
3       2       1       1 3 
4       3       1       1 3 1 
5       3       2       1 1 1 
6       4       1       1 1 3 3 
7       4       4       1 3 5 13 
....
21201   18      131059  1 1 7 11 15 7 37 239 337 245 1557 3681 7357 9639 27367 26869 114603 86317

这里的 $d$ 指维度，可以看到这个文件支持生成最高21201维的点集，每行描述了一个维度的生成矩阵。但并没有直接给出，而是只给出了矩阵的前 $s$ 个数，后续需要我们根据公式自己推出来（具体就不细谈了，可以直接套官网的代码）。

最后再说一下Sobol在渲染中的应用。

例如，一次路径追踪中，要产生8个随机数，那么我们会使用一个8维样本来表达这一整个随机过程，而非使用8个一维样本。

光场

Plenoptic Function（全光函数）：$P(\theta, \phi, \lambda,t,x,y,z)$，指任一个位置，任一时刻向任一方向看到的某波长的光强。一个抽象概念，可以描述整个世界。

Light Field（光场）：全光函数的一个子集，对于一个物体，考虑其包围盒，光场表达从任一位置，向任一方向发出的光（4D，位置和方向都可以用球面坐标表示）

nerf即使用神经网络来拟合这样一个光场（辐射场），来实现重建。

球面谐波函数

基函数：使用一组函数 $b_i(x)$，他们的线性组合可以近似任一其他函数：$f(x)\approx \sum_i^n A_ib_i(x)$

我倾向于将基函数理解成“无限维度的向量”，即每个 $x$ 都是一个维度。

类似于基向量，因为维度是无限的，故希望不是近似而是完全匹配任一函数的话，需要无限个基函数：$f(x)=\sum_i^{\infty} A_ib_i(x)$

函数的乘积积分(Product integral) 类似于向量点乘，故基函数的正交性类似于：$\int f(x)g(x)d_x=0$ 对其中任两个基函数都成立。

回到球面谐波函数上来，它是一组定义在球面上的基函数 $r=b_i(\theta, \phi)$，它是正交的。

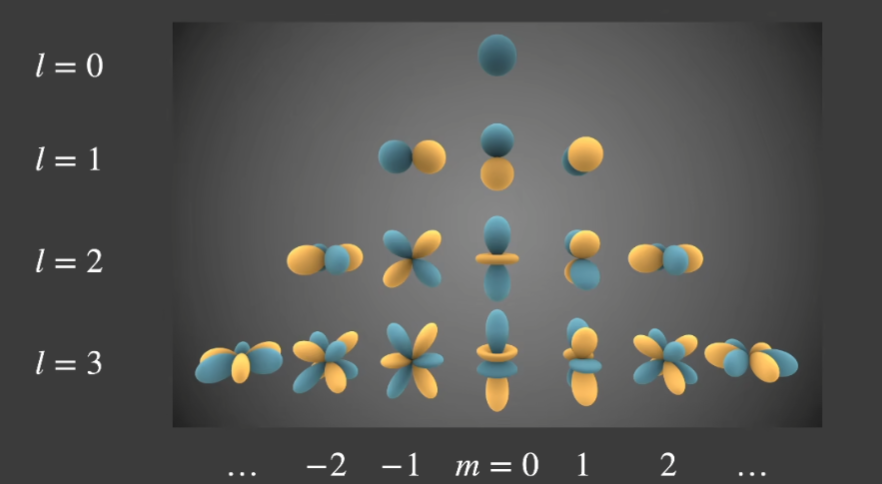
如图所示，球谐函数可以使用若干阶，越高阶频率越高，越能表现函数细节，通常使用前3阶即可比较好的近似。

近似 $f(w)$ 时，对于每个基函数前的系数，可以这样计算：$c_i=\int_\Omega f(w)b_i(w)d_w$

这称为“投影”，从上述基向量的角度来看非常显然。

应用

取低阶的SH可以拟合一个球面光照（如环境光），类似一种低通filter

对于漫反射材质，其反射的主要是低频光照信息，仅需使用3阶SH拟合环境光，就能取得极其近似的效果。

球面高斯函数

定义：
$$
G(\vec n,\vec v, a, \lambda)=ae^{\lambda(\vec n \cdot \vec v - 1)}
$$
高斯分布，即正态分布，距离轴线越远函数值越小。球面高斯函数（SG）将这种分布迁移到了三维球面上，用以表示一个波瓣。以 $\vec n$ 定义波瓣的中心方向，$\lambda$ 系数定义波瓣的”胖瘦“，$a$ 对波瓣进行整体缩放。这些从上式中不难看出。

SG的特点：

• 它的积分是封闭形式的
• 两个SG的乘积仍然是SG，因此两个SG的点积也是封闭形式
• …

我们也可以定义一组SG基函数，通过调整他们的参数和系数来混合成新的球面函数。但SG有两个问题：它是各项同性的，且随意的一组SGs很难正交。

一组SH基函数能够快速拟合一个任意函数（求出系数组），利用的是对正交基的“投影”。SGs没了正交性，这个过程的复杂度将不可接受。故SGs基函数的数量不能很多。

ASG

Xu 2009

各向异性的SG，定义为：
$$
G(\vec v,[\vec x, \vec y, \vec z], [\lambda, u], c)=c\cdot max(v\cdot z, 0) \cdot e^{-\lambda(v\cdot x)-u(v\cdot y)}
$$
定义也比较直观，波峰在 $\vec v=\vec z$ 处，其中 $\vec x,\vec y, \vec z$ 是一个三维空间下的正交基。

原SGs也可以拼出各向异性的球面函数，但需要非常多的SG，而使用ASGs则可以使用一组数量较少的基函数。

颜色

Spectral Power Distributions (SPD)：各个波长上分布的光强，多个光叠加时，SPD也可以叠加（线性性质）。

同色异谱：不同分布的光谱，人看起来可能是一样的（三种视锥细胞各自感应的结果）

Irradiance map

可以认为：环境贴图、面积光的数值单位都是irradiance，因为其描述的是一个微面发出的总的辐射（无方向性），取任意方向就是radiance

但irradiance map说的irradiance并不是这个，它通常用来做间接光预积分。

由于漫反射部分BRDF通常与wo无关（Lambertain项），可以从积分中分离，那么剩下的部分仅与法线n有关。预积分出对于每个法线n而言的irradiance，存在一张贴图里，就是常说的irradiance map。

烘焙

烘焙操作，通常就是在贴图上保存irradiance信息。

烘焙需要先进行一波展UV，得到UV2，这个UV2它保证不重复，而原来的UV就不一定了。

烘焙，逐物体操作，每个mesh丢入管线，顶点着色器输出的裁剪坐标直接为UV2，而计算仍然在世界空间下进行，方便地得到纹理空间的烘焙结果。

画饼

视差贴图（法线贴图进阶）

B样条曲线

微分方程、RungeKutta方法

Spatial hash?