Volume rendering概述

\[ \newcommand{\w}{\pmb\omega} \newcommand{\vec}{\mathbf} \]

Radiative Transfer Equation, RTE

考虑光线沿 \(\w\) 方向传播，经过参与介质中一段微分距离 \(d\vec x\) 时，radiance的变化率：

\[ \nabla L(\vec x, \w) = -\sigma_t L(\vec x, \w) + \sigma_aL_e(\vec x, \w) + \sigma_s\int_{S^2}f_p(\vec x,\w,\w')L(\vec x, \w')d\w' \] 其中：

\(\sigma_a\) 为吸收系数，\(\sigma_s\) 为散射系数。

\(\sigma_t = \sigma_a + \sigma_s\)，即衰减系数；\(\frac{\sigma_s}{\sigma_t}\) 为反照率，albedo。

注意这些 \(\sigma\) 系数都是定义在导数上的，衡量的都是变化率，而不是发生吸收/散射的比例，因此他们都可以大于1。

介质可以由 \(\sigma_a, \sigma_s\) 定义，也可以等效地由 \(albedo, \sigma_t\) 定义，两组参数可以相互转换。

\(L_e\) 为介质的自发光。

\(f_p\) 为Phase function，\(f_p(\w_i \rightarrow \w_o)\) 表示 \(\w_i\) 入射的光发生散射后，散射到 \(\w_o\) 方向的比例，和BRDF不同，它直接就是归一化的，并且有可逆性： \[ \begin{gather*} \int_\Omega f_p(\w_i, \w_o) d\w_o = 1 \\ \sigma_s(\w_i) f_p(\w_i, \w_o) = \sigma_s(\w_o) f_p(\w_o, \w_i) \end{gather*} \] 在均匀的各项同性介质中，\(f_p\) 与位置和方向无关，只与 \(\w_i,\w_o\) 之间的夹角有关，可以视为一维函数 \(f_p(\theta)\)，更简单地，Phase function也可以是各项同性的：\(f_p = \frac{1}{4\pi}\)

上述的各个 \(\sigma\) 在非均匀/各项异性介质中，也可能是位置/角度的函数。

Volume Rendering Equation, VRE

VRE即RTE的积分形式，考虑光线在介质中传播一段距离，得到的radiance（注意这也包括了这段路径上，每一处接收到的来自其他方向的散射 \(L_s\)，因此这是一个二重的积分，一维是距离，一维是方向） \[ \begin{gather*} L(\vec x, \w) = \int_0^z T(\vec x, \vec y)[\sigma_a L_e(\vec y,\w) + \sigma_s L_s(\vec x, \w)]d\vec y \\ L_s(\vec x, \w) = \int_{S^2}f_p(\vec x,\w,\w')L(\vec x, \w')d\w' \\ T(\vec x, \vec y) = exp(-\int_y^x \sigma_t(s) d_s) \end{gather*} \] 上面比较重要的东西是 \(T\)，被称为衰减项（attenuation，或光学厚度，transmittance等），表示光线在介质中行进一段距离后，有多少比例直接透过（没有发生散射和吸收）。

我们知道，光线在经过一段微分距离时，因散射或透射而损失的量为： \[ dL(\vec x, \w) = -\sigma_t(\vec x) L(\vec x, \w) d\vec x \] 这里我特意没有写成 \(\frac{dL}{d\vec x}\) 的形式，是为了提醒一件事：\(\sigma_tL\) 并非衰减量，而是衰减量关于当前位置的导数。\(\sigma_t\) 并非衰减比例，而是一个衰减速度。同理，其他 \(\sigma\) 也都是在导数意义下定义的，因此它们都可以大于1。

回到这个式子上，它是一个微分方程，解出来结果是： \[ L(\vec x, \w) = L_0 e^{-\int_0^\vec x \sigma_t(\vec x)d\vec x} \] 我们关注光线传播一定距离 \(t\) 产生的衰减比例 \(T(t)\)： \[ T(t) = exp(-\int_0^t\sigma_t(x)dx) \] 它才是一个范围在 \((0, 1]\) 之间的数；\(1-T(t)\) 即为在 \(t\) 以内发生碰撞的概率，或者说是碰撞概率的 \(CDF\)。

那么可以计算恰好在 \(t\) 点发生碰撞的概率 \(pdf(t)\)： \[ pdf(t) = \frac{d(1-T(t))}{dt} = \sigma_t(t)T(t) \] 回到VRE上： \[ L(\vec x, \w) = \int_0^z T(\vec x, \vec y)[\sigma_a L_e(\vec y,\w) + \sigma_s L_s(\vec x, \w)]d\vec y \\ \] 用蒙特卡洛法求解VRE，也就是需要对距离和方向进行采样，方向可以根据phase function采样，距离采样如下。

Sample distance

均匀情况下，我们已经有了 \(pdf\) 表达式，可以轻松用逆变换方法采样 \[ CDF^{-1}(t) = \frac{ln(1-\xi)}{-\sigma_t} \] \(\xi\) 为0-1之间的随机数。

若发生散射，则再对phase function作重要性采样决定散射方向。

非均匀情况下，有一些手段。

这里的几种方法都是先根据随机数，决定 \(CDF(t) = \xi\)，然后再去找这样的 \(t\) 的位置（包括ray marching法），它们并没有改变按 transmittance 采样的本质。

若介质在光线路径上可以分为几段（例如常见的网格表示的体数据），则可以分段采样。
Ray marching方法，均匀步长。它并不是指每一步采样距离都相等，还是先决定 \(CDF(t) = \xi\)，然后用均匀步长去找这个 \(t\)（感觉很呆），而且也是有偏的，它将每一步内的介质都近似为均匀。
Woodcock tracking，虚点法，可以认为是一种拒绝采样策略。它首先将介质每一处的衰减项都放大为 \(\sigma_t^{max}\) ，构成均匀介质，然后在采样到一点 \(t\) 时，以 \(\frac{\sigma_t(t)}{\sigma_t^{max}}\) 的概率接受，否则拒绝。数学上可以证明它是无偏的。

非均匀介质的另一个问题是给定起始点位置，计算 \(T(x,y)\)。它的解法和Sample distance非常类似，同时还可以直接蒙特卡洛解。

在实际计算中，光线会有一个最大行进距离 \(t_{max}\)（例如可能撞到实体表面），Sample distance时，有 \(T(t_{max})\) 的概率采样到超过这个距离的值，需要进行特判。

Microflake model

在上文中，我们并不假设“介质”是由什么组成的，它仅仅是由几个 \(\sigma\) 和Phase function定义，而Microflake是一种常见的具体的参与介质的实现方式，将参与介质看做由无数微小的，随机朝向的镜面薄片组成，类似微表面模型，使用 \(D(\w_m)\) 表示朝向 \(\w_m\) 的微薄片比例。

推导 \(\sigma_t\)

先写一个通俗但不太对的理解：

设微薄片的密度为 \(\rho\)，\(\w\) 方向上微薄片的平均投影面积为 \(\sigma(\w)\) \[ \sigma(\w) = \int_{S^2} <\w_m, \w>D(\w_m) d\w_m \] 假设微薄片在各个方向上都不重叠，则单位体积中，被遮挡的比例为： \[ \sigma_t(\w) = \rho \sigma(\w) = \rho\int_{S^2} <\w_m, \w>D(\w_m) d\w_m \] 这个理解有很多槽点，首先我们已经说过 \(\sigma_t\) 并不是被遮挡的比例，而是衰减的速度，定义为 \(\frac{dL}{d\vec x} = -\sigma_t L\)；

其次，由于微薄片可以无限小，\(\rho\) 和 \(\sigma\) 的数值含义也并不明确。

我认为更合理的理解：

设微薄片的密度为 \(\rho\)，\(\w\) 方向上的平均投影面积为 \(\sigma(\w)\)，设微薄片的面积为1单位 \[ \sigma(\w) = \int_{S^2} <\w_m, \w>D(\w_m) d\w_m \] 考虑光线穿过一个1单位面积、长 \(d\vec x\) 的微分圆柱，辐射的变化量： \[ \begin{gather*} -d L = L\sigma_t(\w)d\vec x=L\sigma(\w)\rho d\vec x \\ \sigma_t(\w) = \rho\sigma(\w) \end{gather*} \] 这里，\(\rho d\vec x\) 给出了微分圆柱中的微薄片数量，而在微分圆柱中，总投影面积给出了光线在此处被遮挡的比例；这种思路能够推导出正确的结果，并且逻辑上更加合理。

关于 \(\rho\)，这里实质上的定义为：单位体积内微薄片的面积，想象每个微薄片都是1单位，\(\rho\) 衡量数量会更加直观；\(\sigma\) 实质定义为单位面积的微薄片在投影后的面积，也即投影产生的平均面积缩放比例。

推导Phase function

首先定义在特定方向 \(\w_i\) 上的可见法线分布为： \[ \begin{gather*} D_{\w_i}(\w_m) = \frac{D(\w_m)<\w_i\cdot \w_m>}{\sigma(\w_i)} \\ \int_{S^2} D_{\w_i}(\w_m)d\w_m = 1 \end{gather*} \] 它一定是归一化的，可以对它进行采样。

广义上，微薄片不一定要是镜面，它可以有一个小的BRDF，我们定义micro-phase function：\(p(\w_m,\w_i\rightarrow \w_o)\)，指特定方向的小微薄片的BRDF，那么宏观Phase function定义为： \[ f_p(\w_i\rightarrow \w_o) = \int_{S^2} p(\w_m,\w_i\rightarrow \w_o) \cdot D_{\w_i}(\w_m)d\w_m \] 通常只会考虑镜面微薄片，仅当 \(\w_h = \w_m\) 时： \[ p(\w_m,\w_i\rightarrow \w_o) = \frac{1}{4|\w_i\cdot \w_h|} \] 容易得到： \[ f^{spec}_p(\w_i\rightarrow \w_o) = \frac{D(\w_h)}{4\sigma(\w_i)} \] 由于albedo、density都与方向无关，则 \(\sigma_s\) 正比于 \(\sigma_t\) 正比于 \(\sigma\)，因此这个Phase function也满足可逆性约束 \(\sigma_s(\w_i) f_p(\w_i, \w_o) = \sigma_s(\w_o) f_p(\w_o, \w_i)\)

SGGX

一种具体的，易于控制的法线分布 \(D(\w_m)\)。

SGGX使用一个3x3的正定对称矩阵 \(S\) 描述了一个椭球： \[ S = (\w_1, \w_2, \w_3) \left( \begin{matrix} S_{11} & 0 & 0\\ 0 & S_{22} & 0\\ 0 & 0 & S_{33} \end{matrix} \right) (\w_1, \w_2, \w_3) ^T \] \(\w_1, \w_2, \w_3\) 是椭圆的三个轴，这里看似是用一个transform矩阵定义椭球。但实际上是另一种定义。

用二次型来定义椭球，椭球上的点 \(P\) 有 \[ P^TSP = \frac{\sqrt{|S|}}{\pi} \] 需要注意式子右边并不是常见的1，它相当于为椭圆的三个轴添加了同一个缩放，可能是为了让椭球在某方向的投影面积更易于表示？

椭球长这样：

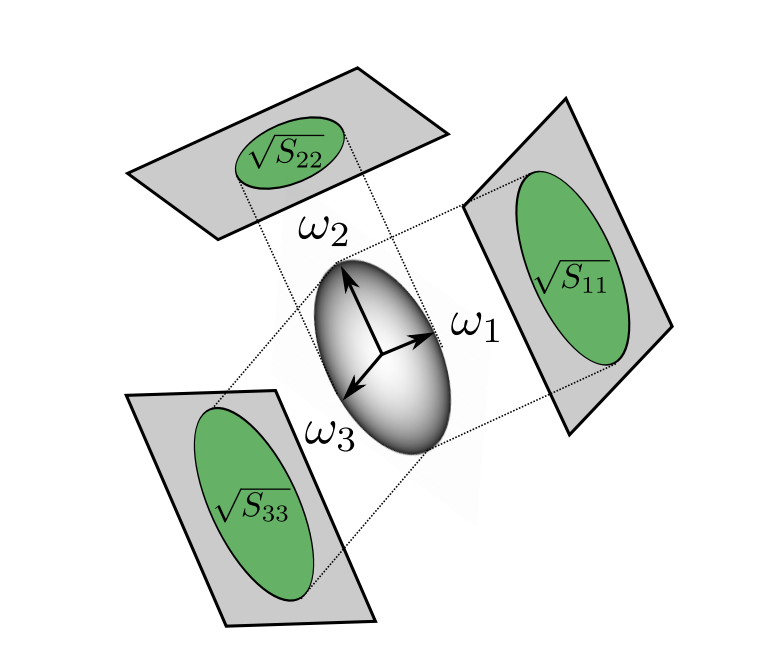
前面忘了后面忘了，任意方向 \(\w_i\) 的投影为： \[ \sigma(\w_i) = \sqrt{\w_i^TS\w_i} \] 表面法线（unnormalized）： \[ \frac{\partial (P^TSP)}{\partial P} = 2SP \] 法线分布为： \[ D(\w_m) = \frac{1}{\pi \sqrt{|S|}(\w_m^TS^{-1}\w_m)^2} \] 这里我们拿到了需要的 \(D(\w_m)\) 和 \(\sigma(\w)\)，可以想象微薄片的分布满足椭球表面分布（我会把整个椭球想象成是一个微薄片，光线会根据VNDF随机击中椭球上的一点，这也是等价的）

SGGX使用的 \(D(\w_m)\) 是非归一化的，\(D\) 的缩放会导致 \(\sigma\) 等比缩放，并不影响Phase function；对 \(\sigma_t\) 而言，它会等比被放大，可以想象这是对 \(\rho\) 的缩放，没什么大影响，但会一定程度上导致 \(\rho,\sigma\) 的数值脱离其原本的物理含义（反正这几个参都是调的所以无所谓吧（。

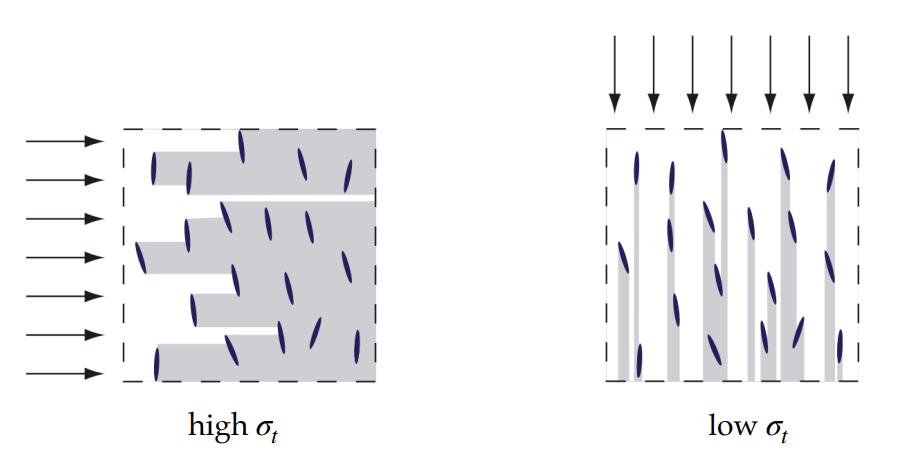
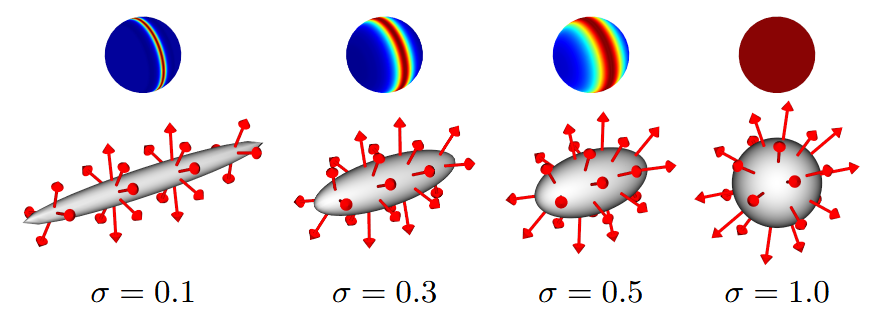
应用举例：用SGGX来做fiber的分布，fiber是条状的，我们可以更简单地使用一个粗糙度参数 \(\alpha\) 控制fiber椭球的形状。 \[ S = (\w_1, \w_2, \w_3) \left( \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & \alpha^2 \end{matrix} \right) (\w_1, \w_2, \w_3) ^T \]

SpongeCake

SpongeCake其实是表面材质，但他是基于Volume推导得到的。

主要有两点假设：

Position-free，光线的入射和出射在同一个位置（同一像素内），因此介质可以视作均匀的，光线是平行的。
忽略层与层之间界面，即光线穿过层与层之间时方向不会发生改变。

回顾一下，镜面微薄片有： \[ f^{spec}_p(\w_i\rightarrow \w_o) = \frac{D(\w_h)}{4\sigma(\w_i)} \] 为了简便，我们定义： \[ \hat f_p(\w_i, \w_o) = \sigma_t(\w_i)f_p^{spec}(\w_i, \w_o)F(\w_h) = \frac{\sigma_t(\w_i)D(\w_h)F(\w_h)}{4\sigma(\w_i)} \] 这里把 \(\sigma_t\) 和菲涅尔项一起包进来了，记得 \(\sigma_t \times albedo = \sigma_s\)，\(\hat f_p\) 是可逆的。

由于 \(\sigma_t(\w_i) = \rho\sigma(\w_i)\)： \[ \hat f_p(\w_i, \w_o) = \frac{\rho D(h)F(h)}{4} \]

注意：菲涅尔项的含义是：反射光的比例，另一部分是折射（被吸收）了，而不是穿过去了！SpongeCake是一个表面模型，下文要考虑的Transmission也只是穿过这个表面的光线，而不是被折射的光线。故可以发现下面用的还是 \(F(h)\) 而非\(1 - F(h)\)

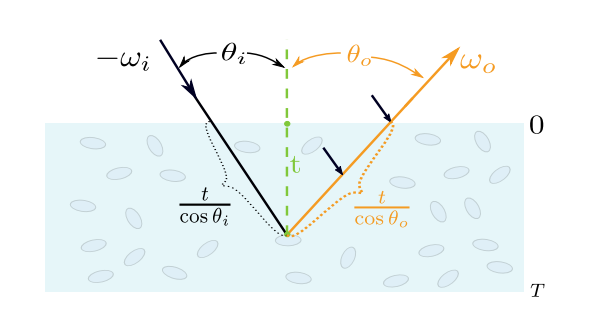
考虑在深度上的积分： \[ \begin{gather*} f_r(\w_i, \w_o) = \int_o^T \frac{\hat f_p(\w_i, \w_o)}{cos(\w_i)cos(\w_o)} \tau(\w_i,\frac{t}{cos(\w_i)}) \tau(\w_o,\frac{t}{cos(\w_o)}) dt \\ \tau(\w, l) = e^{-\sigma_t(\w)l} \end{gather*} \] 其中 \(\tau\) 即体渲染中的Transmittance，扩展到了各项异性，为了避免符号冲突在这边改成了 \(\tau\)；

分母项的 \(cos(\w_i)\) 来自于brdf的定义，\(cos(\w_o)\) 是因为体渲染积分本身是在出射光线上积的，要将积分域转换到深度上。

上面这个积分是可以直接解出来的： \[ \begin{align*} f_r(\w_i, \w_o) &= \frac{\hat f_p(\w_i, \w_o)}{cos(\w_i)cos(\w_o)} \int_o^T \tau(\w_i,\frac{t}{cos(\w_i)}) \tau(\w_o,\frac{t}{cos(\w_o)}) dt \\ &= ... \\ &= \frac{D(\w_h)F(\w_h)G(\w_i, \w_o)}{4cos(\w_i)cos(\w_o)} \\ \end{align*} \] 其中： \[ \begin{align*} G(\w_i, \w_o) &= \frac{1 - exp(T\rho(\Lambda(\w_i) + \Lambda(\w_o)))}{\Lambda(\w_i) + \Lambda(\w_o)}\\ \Lambda(\w) &= \frac{\sigma(\w)}{cos(\w)} \end{align*} \] 推导过程中套入了 \(\sigma_t = \sigma \rho\)，中间推导不难不想码了）

这样就有了一个类似传统BRDF的形式，只需要更改法线分布和 \(G\) 项。

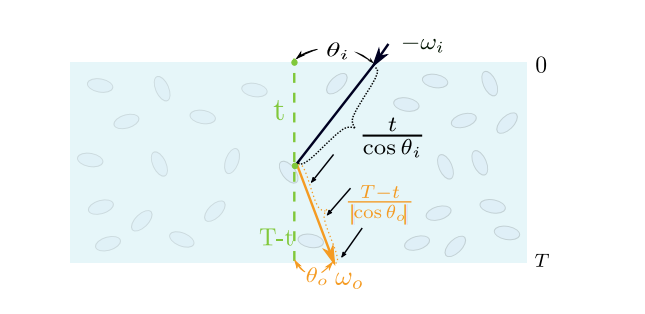
考虑透射，也非常简单：只需更改上述积分的一段长度，推导容易得到： \[ G(\w_i, \w_o) = \frac{1 - exp(T\rho(\Lambda(\w_i) + \Lambda(\w_o)))}{\Lambda(\w_i) + \Lambda(\w_o)} \cdot exp(T\rho\Lambda(\w_o)) \] 其中 \(cos(\w_o \lt 0)\)，已经考虑到。

多层情况

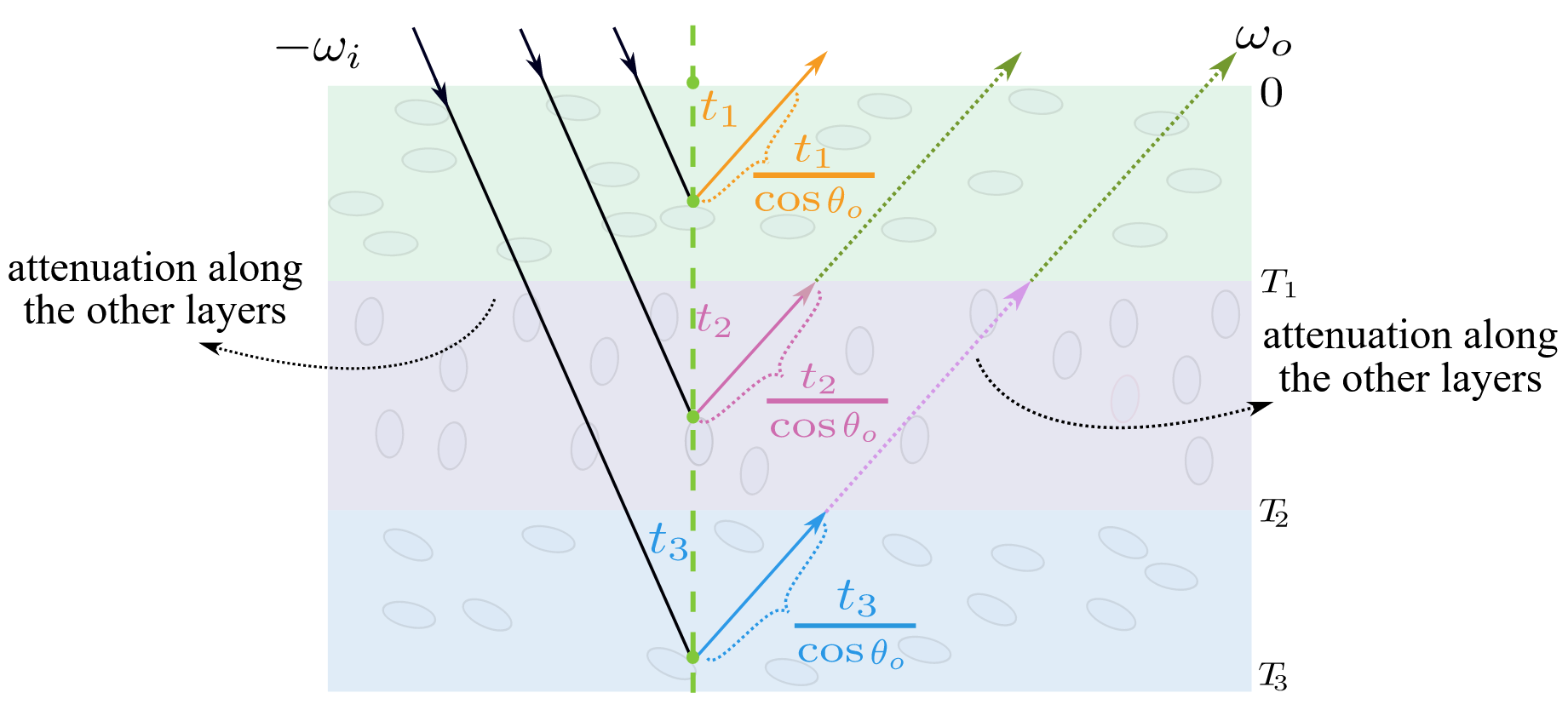
多层情况下，依次考虑每一层的贡献，并乘上光线在其他几层的衰减。例如，图中紫色层的贡献为： \[ \tau(\w_i, \frac{T_1}{cos(\w_i)}) \tau(\w_o, \frac{T_1}{cos(\w_o)})f^{T_1\rightarrow T_2}_r(\w_i, \w_o) \] 其它层和透射情况同理。

采样

虽然看起来像体渲染，但实际上距离积分被我们解出来了，只剩下角度一维；而介质又是均匀的，单层情况下直接按Phase function采样得到出射方向即可。

多层情况，需要先采样得到在哪一层发生了散射，这里又可以利用Transmittance了。以图为例：

\(1-\tau(\w_i, \frac{T_1}{cos(\w_i)})\) 即为在第一层发生散射的概率；

\(\tau(\w_i, \frac{T_1}{cos(\w_i)})(1-\tau(\w_i, \frac{T_2-T_1)}{cos(\w_i)}))\) 即为穿过第一层，在第二层发生散射的概率；

以此类推，最终还能够得到一个全部穿过的概率，我们可以用它来采样得到一个直接透射分量。

总结

Volume Rendering是基于RTE进行渲染，可以代入任意介质，而一个介质由Phase Function以及 \(\sigma_t, albedo\)（也可以等效为 \(\sigma_a, \sigma_s\)）定义，其中Phase function影响散射，各种 \(\sigma\) 系数影响传播，Phase function与medium的sample distance, transmittance均无关。

Microflake是一种介质模型，可以代入任意形式的微薄片，需要的是法线分布 \(D\) 以及密度 \(\rho\) ，通过他们推导Phase Function和 \(\sigma_t\)

SGGX给出了一种具体的容易控制的法线分布 \(D\)

SpongeCake则是一种从一定厚度的介质中推导得到的表面模型，可以代入任一种Microflake。