Volume rendering

Volume Rendering考虑参与介质（如雾、烟等）中的光线传播情况。

辐射传输方程

Radiative Transfer Equation, RTE

考虑光线穿过参与介质中 $p$ 点时，radiance的变化量：

大致形式：
$$
L_o - L_i = -\sigma_t \cdot L_i + L_e + \sigma_s\int_{S^2}f_pL_jdw_j
$$
其中：

$\sigma_a$ 为吸收系数，表示光线被介质吸收的比例。

$\sigma_s$ 为散射系数，表示光线被散射到其他方向的比例。

$ \sigma_t = \sigma_a + \sigma_s$，即光线撞击到粒子的比例。

$f_p$ 为Phase function，$f_p(w_i \rightarrow w_o)$ 表示 $w_i$ 入射的光发生散射后，散射到 $w$ 方向的比例。注意，$f_p$ 仅衡量散射性质，而入射光并不都发生散射。因此，$L_o \leftarrow \sigma_t f_pL_i$。事实上，$f_p$ 也需要带上 $\sigma_t$ 才可逆。

$L_e$ 为介质的自发光。

通常在推导时会用到反照率 albedo，它等于 $\frac{\sigma_s}{\sigma_t}$

大部分情况下我们都考虑均匀介质，不均匀介质则还需在各个函数中加入参数 $p$

Volume Rendering

对RTE的具体估计，使用蒙特卡洛方法。

考虑最简单的均匀各向同性介质情况，$\sigma_t $ 是一个常数

经过 $d_x$，能量损耗为：
$$
dL = L_i(-\sigma_td_x)
$$
求解这个微分方程，我们抄来结果：
$$
L = e^{-\sigma_tx}
$$
这是经过 $x$ 距离后的光线余量（不限制距离）。

可以用这个式子作为光线传播到 $x$ 还未被吸收或折射的概率，当然要将概率归一化到1：
$$
pdf(x) = \frac{e^{-\sigma_tx}}{\sigma_t} \
\int_0^{\infty} pdf(x)d_x = 1
$$
重要性采样，推得
$$
CDF^{-1}(x) = \frac{ln(1-y)}{-\sigma_t}
$$
$y$ 替换成0-1之间的随机数，即可完成抽样。

若发生散射，则再对phase function作重要性采样决定散射方向。

这是在体积介质中做蒙特卡洛路径追踪的基本原理，可以扩展到各项异性、不均匀介质中。

Phase function

重复一下，Phase function $f_p(w_i\rightarrow w_o)$ 定义为散射到 $w_o$ 的能量与所有散射能量的比值，它是归一化的。
$$
\int_{S^2} f_p(w_i\rightarrow w_o) dw_i = 1
$$

另外，散射到 $w_o$ 的能量与所有入射能量的比值定义为 $f_a(w_i\leftrightarrow w_o)$，它不是归一化的，但具有可逆性。
$$
f_a(w_i\leftrightarrow w_o) = f_p(w_i\rightarrow w_o) \cdot \sigma_s(w_i)
$$
在均匀的各项同性介质中，$f_p$ 与位置和方向无关，只与 $w_i,w_o$ 之间的夹角有关，可以视为一维函数 $f_p(\theta)$，更简单地，相函数也是各项同性的情况：$f_p(\theta) = \frac{1}{4\pi}$

Microflake model

这是一种各项异性的体积模型，将参与介质看做由无数微小的，随机朝向的薄片组成，类似微表面模型，使用 $D(m)$ 表示朝向 $m$ 的微薄片分布。

我们可以具体将 $D(m)$ 定义为朝向 $m$ 的微薄片面积与宏截面的比例，这种定义与微表面类似，但它不是归一化的（和微表面不同，薄片间存在间隙），不能直接用作pdf。

注意，一个微薄片可以有很多个方向的法线，取决于具体的形状。

单个微薄片在 $w_i$ 方向的投影面积定义为
$$
\sigma(w_i) = \int_{S^2} D(m) <w_i\cdot m> d_m
$$
这里的 $\sigma$ 没有下标，为单个薄片的投影面积，和前文中表示光线比例的 $\sigma_t$ 等区分（许多经典文献中的符号都是这样，因此尽管容易混淆还是不作更改。）

归一化到投影面上：
$$
D_{w_i}(m) = \frac{D(m)<w_i\cdot m>}{\sigma(w_i)} \
\int_{S^2} D_{wi}(m)dm = 1
$$
这里的 $D_{w_i}(m)$ 被称为Visible normal。

广义上，微薄片不一定要是镜面，它可以有一个小的BRDF，我们定义micro-phase function：$p(m,w_i\rightarrow w_o)$，指特定方向微薄片的phase function，那么有：
$$
f_p(w_i\rightarrow w_o) = \int_{S^2} p(m,w_i\rightarrow w_o) \cdot D_{w_i}(m)d_m
$$
如果认为所有微薄片都是镜面，推导Specular phase function：

仅当 $h=m$ 时有：
$$
p(m,w_i\rightarrow w_o) = \frac{1}{4|w_i\cdot w_h|}
$$
代入得到：
$$
f^{spec}_p(w_i\rightarrow w_o) = \frac{D(h)}{4\sigma(w_i)}
$$

另外，$w_i$ 方向的光线撞击到粒子的比例有：
$$
\sigma_t(w_i) = \rho \sigma(w_i)
$$

SpongeCake

SpongeCake其实是表面材质，但他是基于Volume推导得到的。

使用Microflake模型表达Volume，简化地认为所有flake都是镜面，不考虑吸收和漫反射，可以直接使用上述 $f_p=f_p^{spec}$ 的形式

上面提到过，定义为散射光与入射光比值的phase function具有可逆性，我们再额外考虑菲涅尔效应，得：
$$
f_a(w_i\rightarrow w_o) = f_p(w_i\rightarrow w_o)F(h) \sigma_t(w_i) = \frac{D(h)F(h)\sigma_t(w_i)}{4\sigma(w_i)}
$$
由于 $\sigma_t(w_i) = \rho\sigma(w_i)$
$$
f_a(w_i \rightarrow w_o) = \frac{\rho D(h)F(h)}{4}
$$

注意：菲涅尔项的含义是：反射光的比例，另一部分是折射（被吸收）了，而不是穿过去了！

SpongeCake是一个表面模型，下文要考虑的Transmission也只是穿过这个表面的光线，而不是被折射的光线。故可以发现下面用的还是 F(h) 而非1 - F(h)

考虑整个部分的贡献，可以写出下面的积分式：
$$
f_r(w_i \rightarrow w_o) = \int_o^T \frac{f_a(w_i \rightarrow w_o)}{cos(w_i)cos(w_o)} \cdot att(w_i,t)\cdot att(w_o,t) \cdot d_t \
att(w,t) = exp
\left(
-\frac{t}{cos(w)} \sigma_t(w)
\right)
$$
其中 $att$ 指的是一个方向上的衰减，使用上文体渲染中推导出的式子，分母项的 $cos(w_i)$ 来自于brdf的定义，$cos(w_o)$ 是因为体渲染积分本身是在出射光线上积的，要将积分域转换到深度上。

由此代入，我们得到了下面形式：
$$
f_r(w_i \rightarrow w_o) &=& \frac{\rho D(h)F(h)}{4cos(w_i)cos(w_o)} \int_o^T att(w_i,t)\cdot att(w_o,t) \cdot d_t \
&=&…\
&=& \frac{D(h)F(h)G(w_i, w_o)}{4cos(w_i)cos(w_o)}
$$
其中：
$$
G(w_i, w_o) &=& \frac{1 - exp(T\rho(\Lambda(w_i) + \Lambda(w_o)))}{\Lambda(w_i) + \Lambda(w_o)}\
\Lambda(w) &=& \frac{\sigma(w)}{cos(w)}
$$
推导过程中套入了 $\sigma_t = \sigma \rho$，中间不难就不想码了）

这样就有了一个类似传统BRDF的形式，只需要更改法线分布和 $G$ 项。

考虑透射，也非常简单：只需更改上述积分的一段长度，推导容易得到：
$$
G(w_i, w_o) = \frac{1 - exp(T\rho(\Lambda(w_i) + \Lambda(w_o)))}{\Lambda(w_i) + \Lambda(w_o)} \cdot exp(T\rho\Lambda(w_o))
$$
其中 $cos(w_o \lt 0)$，已经考虑到。

SGGX

https://dl.acm.org/doi/abs/10.1145/2766988

这篇文章提出了一种可以自由控制的Microflake分布，使用一个3x3的正定对称矩阵 $S$ 控制一个椭球微片的形态。

$$
S = (w_1, w_2, w_3)
\left(
\begin{matrix}
S_{11} & 0 & 0\
0 & S_{22} & 0\
0 & 0 & S_{33}
\end{matrix}
\right)
(w_1, w_2, w_3) ^T
$$
$w_1, w_2, w_3$ 是椭圆的三个轴，这里看似是用一个transform矩阵定义椭球。但文章用了另一种定义。

用二次型来定义椭球，椭球上的点 $P$ 有
$$
P^TSP = \frac{\sqrt{|S|}}{\pi}
$$
因此说矩阵 $S$ 是正定对称的。不过需要注意式子右边并不是常见的1，它相当于为椭圆的三个轴添加了同一个缩放，可能是为了让椭球在某方向的投影面积更易于表示？

椭球长这样：

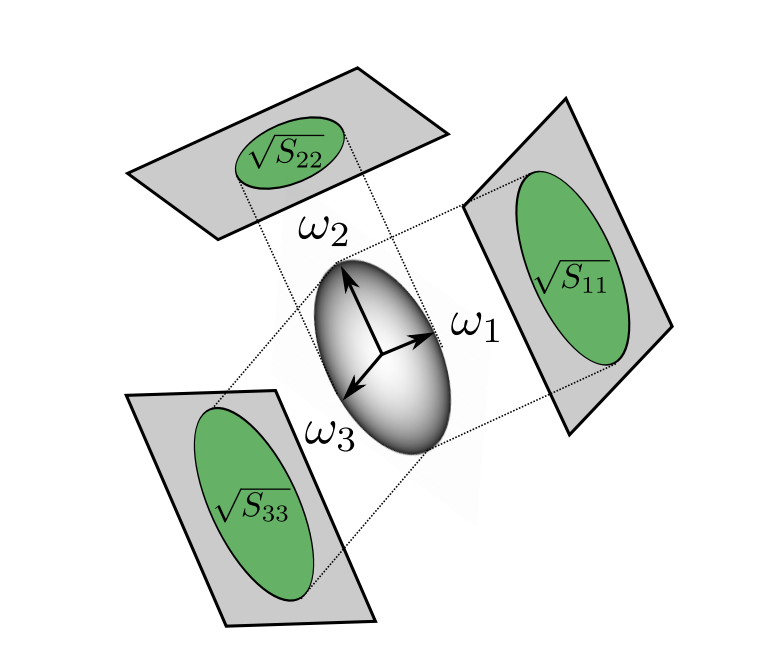
如果仅考虑 $P^TSP$ 对应的标准型（即忽略旋转），我们得到椭球的表达式：
$$
S_{11}x^2 + S_{22}y^2 + S_{33}z^2 = \frac{\sqrt{|S|}}{\pi}
$$
先推导这个椭球在x轴（即旋转后的 $w_1$ 轴）的投影 $A_x$，在 $x = 0$ 时：
$$
\frac{S_{22}\pi}{\sqrt{|S|}}y^2 + \frac{S_{33}\pi}{\sqrt{|S|}}z^2 = 1 \
A_x = \sqrt{S_{11}}
$$
任意方向 $w_i$ 的投影：（推导跳了先（
$$
\sigma(w_i) = \sqrt{w_i^TSw_i}
$$
表面法线（unnormalized）：
$$
\frac{\partial P^TSP}{\partial P} = 2SP
$$
法线分布：（推导跳了（
$$
D(w_m) = \frac{1}{\pi \sqrt{|S|}(w_m^TS^{-1}w_m)^2}
$$
应用举例：在SpongeCake模型中，用SGGX来做fiber的分布，fiber是条状的，我们可以更简单地使用一个 $\alpha$ 参数控制fiber形状。
$$
S = (w_1, w_2, w_3)
\left(
\begin{matrix}
1 & 0 & 0\
0 & 1 & 0\
0 & 0 & \alpha^2
\end{matrix}
\right)
(w_1, w_2, w_3) ^T
$$

梳理

Volume Rendering是基于RTE进行渲染，可以代入任意介质，仅需介质的Phase Function以及 $\sigma_t$ 等等；

Microflake是一种介质模型，可以代入任意形式的微薄片，SGGX是Microflake的一种具体实现，通过正定矩阵定义了微薄片的 $D(h), \sigma$ ，再加上介质中微薄片的 $\rho$，通过他们推导Phase Function和 $\sigma_t$

Microflake也有一些不同的实现模型，它仅仅只是一种描述微薄片的思想。