ReSTIR学习笔记

2024.2.18 学到了一些新的关于IS和MIS的理解，故在学习ReSTIR前重新整理一遍。

参考：https://zhuanlan.zhihu.com/p/670309912

重要性采样

考虑随机变量 \(\frac{f(x)}{p(x)}\)，\(p(x)\) 为我们选取的任意一个pdf。随机变量的期望为： \[ E(\frac{f(x)}{p(x)}) = \int \frac{f(x)}{p(x)}p(x) dx = \int f(x) dx \] 可以将求积分问题转为求随机变量的期望，估计此期望很简单： \[ I_{IS} = \frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{p(x_i)} \] 这就是蒙特卡洛估计的原理，要使这个估计的方差尽可能小，即要求 \(\frac{f(x)}{p(x)}\) 的期望尽可能小，故 \(p(x)\) 要尽可能接近 \(f(x)\)。

多重重要性采样

被积函数很多时候很复杂，我们没办法用一个简单的 \(p(x)\) 近似它，但存在多个pdf： \(p_1(x),p_2(x)...p_m(x)\)，每个pdf和 \(f(x)\) 的一部分近似。MIS提供了一种多种采样策略结合的方案。

考虑随机变量 \(w_i(x)\frac{f(x)}{p_i(x)}\)，这个随机变量的期望为： \[ E(w_i(x)\frac{f(x)}{p_i(x)}) = \int w_i(x)f(x) dx \] 将M种随机变量对应的期望加起来，又变成了所求积分： \[ \sum_{i=1}^M E(w_i(x)\frac{f(x)}{p_i(x)}) = \int \left ( \sum_{i=0}^M w_i(x) \right ) f(x) dx = \int f(x) dx \] 于是我们得到了MIS的估计式： \[ I_{MIS} = \sum_{i=1}^M \frac{1}{N_i}\sum_{j=1}^{N_i} w_i(x) \frac{f(x)}{p_i(x)} \] 通常的MIS要求 \(\sum_{i=0}^M w_i(x) = 1\)，这保证了结果是无偏的，同时隐含了这M种采样策略估计的结果，应当等权地相加；相应地在只有1样本情况下，应该等概率地选取这M种采样方式。我们如果启发式地控制采样方式出现的概率，例如，以0.25的概率取光源采样，0.75的概率取BSDF采样，那么就等价于BSDF采样出现了3次，光源采样出现了1次，必须有 \(w_{光源采样}(x) +3 w_{BSDF采样}(x) = 1\)

MIS是有条件的：1. 所有 \(f(x)\) 有值的区域，都必须有某个采样方式能采样到；2. 若 \(p_i(x) = 0\) 则必须 \(w_i(x) = 0\)。第二个条件使用启发式权重时通常都是成立的，第一个条件其实相比重要性采样更宽松，它告诉我们：某些采样方式（例如光源采样）可以只关注一部分区域。

要令MIS的方差尽可能小，其实也就是令 \(p_i(x)\) 与 \(w_i(x)f(x)\) 尽可能接近。按最开始的设定，每个 \(p_i(x)\) 都只有一部分和 \(f(x)\) 匹配较好，通常是用 \(p_i(x)\) 的波峰来匹配 \(f(x)\) 的一个波峰。我们希望在 \(p_i(x)\) 较匹配处，\(w_i(x)\) 取尽可能大值。在不匹配处，\(w_i(x)\) 取尽可能小值，来减小此处造成的方差。因此一个启发式地分配策略就是： \[ w_i(x) = \frac{p_i(x)}{\sum_{j=1}^M p_j(x)} \] 也有平方归一的和其他方式，但都比较感性，没有明显的优劣之分，随便取一种即可。

实际应用

我们可以用MIS重新理解前面的提到的直接间接光划分：将他们也看做两种不同的采样策略的结合。

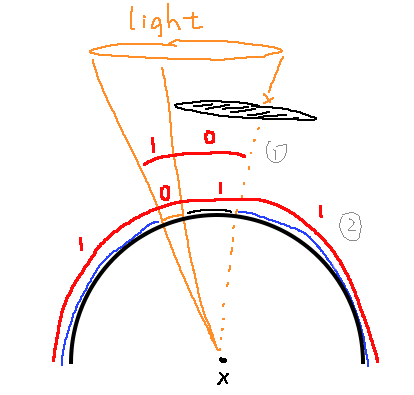
如图所示，红色部分表示直接光采样策略和间接光采样策略，他们在不同区域上被赋予不同的权重（0或1），符合上述MIS要求。

在实际的采样中，我们只能使用一条光线，不可能对 \(M\) 种采样策略都采样一遍，那么就需要从概率上等分它们（注意必须是等分，不能想当然地用其他启发式的划分）。

此时，若我们按照 \(w_i(x) = \frac{p_i(x)}{\sum p(x)}\)，并假设每个采样策略的 \(N_i\) 相同，就会得到一个优美的性质： \[ \begin{align*} I_{MIS} &= \sum_{i=1}^M \frac{1}{N_i}\sum_{j=1}^{N_i} \frac{p_i(x)}{\sum p(x)} \frac{f(x)} {p_i(x)} \\ &= \sum_{i=1}^M \frac{1}{N_i}\sum_{j=1}^{N_i} \frac{f(x)}{\sum p(x)} \\ &= \frac{1}{N}\sum_{j=1}^{N} \frac{f(x)}{\frac{1}{M}\sum p(x)} \end{align*} \] 即，我们可以将多个采样策略合成为一个采样策略，合成的pdf为 \(p_{sum}(x) = \frac{1}{M} \sum p(x)\)，也就是单纯的PDF平均。

注意PDF平均，和各自估计后的结果平均是不一样的，前者等价于MIS，后者是naive的，并无优化。为了区分，这里再写出后者的估计式：\(\frac{1}{M}\sum_{i=1}^M \frac{1}{N}\sum_{j=1}^{N} \frac{f(x)}{p_i(x)}\)，它等价于MIS使用均匀权重。

更一般地，可以有 \(p_{sum}(x) = \sum p_i(x) m_i(x)\)，只要满足 \(\sum m_i(x) = 1\) 即可。这里的 \(m_i(x)\) 是我们选取采样方式 \(i\) 的概率，与 \(w_i(x)\) 不同。

IR (Importance Resampling)

设已有目标PDF为 \(\hat p(x)\)，可以用另一个简单可快速采样的提议PDF \(p(x)\) 来生成接近 \(\hat p\) 分布的样本。

1. 从 \(p(x)\) 中抽取 \(M\) 个候选样本 \(x_1,x_2...x_M\)
2. 样本的初始权重设为：\(w(x_i) = \frac{\hat p(x_i)}{p(x_i)}\)
3. 用归一化后的权重作为概率 \(p_{SIR}=\frac{w(x_i)}{\sum w}\)，从样本集中重新抽取。为了叙述方便，这里将重新抽取的概率分布称为 SIRPDF 。在 \(M\rarr \infty\) 时，SIRPDF符合目标分布 \(\hat p(x)\)

\(M=1\) 时，SIRPDF等于提议分布 \(p(x)\)，\(M\) 越大，SIRPDF越贴近 \(\hat p(x)\)，但不完全相等。不难想到，这种性质很方便我们用来做蒙特卡洛估计，但还有一个问题：我们只知道如何采样SIRPDF，而不知道它的pdf到底是多少。所以需要新的估计式，后文提及。

重采样的优势在于，我们不需要知道 \(\hat p(x)\) 的解析式，甚至不需要 \(\hat p(x)\) 归一化，因为归一化操作隐含在归一化权重中了。或者说，我们可以将任何未归一的分布作为目标，自动得到接近它归一后版本的样本集。

我们可以直接以完整的渲染方程被积项作为 \(\hat p\)，不过后面会说明，实际并不会这样。

（SIR即Sample Importance Resampling，指代IR采集的样本）

RIS (Resampled Importance Sampling)

为什么SIRPDF不能直接用于蒙特卡洛呢？因为pdf没法算，我们根本不知道重采样出来的是啥分布。

RIS提供了一个新的无偏估计公式： \[ I_{RIS} = \frac{1}{N} \sum_{i=1}^N \frac{f(y_i)}{\hat p(y_i)}\frac{\sum_{j=1}^M w(x_j) }{M} \] 其中 \(f(x)\) 是渲染方程的被积项， \(M\) 是提议样本个数，\(N\) 是估计时用的样本个数。无偏性的证明放在后面，可以和RIS+MIS一起理解。

如果令 \(\hat p(x) = f(x)\)，我们会发现这个式子又变回蒙特卡洛了，方差取决于提议分布 \(p(x)\) 的选取。

那么RIS真正的优势在哪里呢？

看一下RIS在Direct light中的应用就明白了：论文原文选取的 \(\hat p\) 为： \[ \hat p = f_s\cdot G\cdot Le \] 是去掉了可见项后的被积项，这个 \(\hat p\) 函数的特点是：接近被积项，计算开销小（因为去掉了最昂贵的遮挡项），同时又不可直接采样（没法直接蒙特卡洛）。

用RIS来处理的话，在 \(M\) 够大，重采样分布能够接近 \(\hat p\) 的情况下，所需的样本数 \(N\) 相比传统IS是有优势的。我们选取计算开销小的 \(\hat p\) 也是为了初始的 \(M\) 个样本权重计算更快。

总结一下的话，最初的RIS其实是一个trade off的方法，通过提高提议数 \(M\) 来减小所需的样本数 \(N\)。效果上也只能说和IS互有优劣。后续提出的复用提议样本的方法，才真正让RIS得以发光发热。

这里偷一个方差公式： \[ V = \frac{1}{M} V(\frac{f(X)}{p(X)}) + (1-\frac{1}{M})\frac{1}{N}V(\frac{f(Y)}{\hat p(Y)}) \] 为了简化，这里假设 \(\hat p\) 是归一化的，如果不是，式子中应为归一化的 \(\hat p\)。

可见，\(M\) 越大，提议分布 \(p\) 越不重要，方差越接近直接用 \(\hat p\) 做蒙特卡洛的结果。，

\(p\) 会影响SIRPDF收敛到 \(\hat p\) 的速度，因此也不能乱取，通常可能会取BSDF之类的好采样的分布。

回忆一下，\(p\) 是一个简单易采样的提议分布，\(\hat p\) 是一个不易采样，但非常接近目标积分的分布。显然我们需要 \[ V(\frac{f(X)}{p(X)}) > V(\frac{f(Y)}{\hat p(Y)}) \] 否则进行重采样没有任何意义；其次，\(\hat p(x)\) 的计算开销也需要显著小于 \(f(x)\)，否则不如直接进行蒙特卡洛采样。

从另一个角度理解，RIS相较于IS其实是提供了一个额外的控制自由度，\(M\)。

RIS的无偏性证明

我们直接考虑最广义的情况：每个提议样本 \(x_i\) 各自使用单独的提议分布 \(p_i\) 采样，\(w_i(x_i) = \frac{\hat p(x_i)}{p_i(x_i)}\)。先说结论：这样取提议样本也是正确的，并且有一个更加广义的形式。下面一起证明：

这一小节我们用 \(p_i\) 表示提议PDF，\(p\) 为通用的概率符号

这里需要先弄清楚几个概率： \[ \begin{gather*} p(\bold x) = \prod_{i=1}^M p_i(x_i),样本集恰为\bold x的概率 \\ p(z|\bold x) = \frac{w(x_z)}{\sum w}, 已知样本集为\bold x的情况下,重抽样到第z个元素的的概率 \\ p(\bold x, z) = p(\bold x) \cdot p(z|\bold x), 样本集为\bold x 且重抽样到第z个元素的概率 \end{gather*} \] 注意，SIRPDF \(p_{SIR}(x_z)\) 并不等于 \(p(\bold x,z)\)，因为可以有多种 \(\bold x, z\) 的组合可以产生 \(x_z\)，如果我们写出 \(p_{SIR}\) 的形式： \[ p_{SIR}(y) = \sum_{i\in Z(y)} \int_{\bold x|x_i=y} p(\bold x, i) d\bold x \] 其中 \(Z(y) = \{i|1\le i\le M \and p_i(y)\gt 0 \}\)，积分域是所有满足 \(x_i=y\) 样本集（相当于限制第 \(i\) 的样本的值，其余样本均自由）。这个式子枚举了所有能够重抽样产生 \(y\) 的情况，并将其概率相加。这才是SIRPDF的完整表达，它没有一个闭合解。

我们需要证明的是估计式无偏， \[ \begin{gather*} \left< I_{RIS}^{1,M} \right> = \frac{f(y)}{\hat p(y)}\frac{\sum_{j=1}^M w_j(x_j) }{M} = f(y)W(\bold x,z),其中 y=x_z\\ W(\bold x,z) = \frac{1}{\hat p(x_z)}\frac{\sum_{j=1}^M w_j(x_j) }{M} \\ \end{gather*} \] 这里，\(W(\bold x,z)\) 是一个随机变量，虽然此时已知 \(x_z=y\)，但仍有有多种组合能够满足这一约束，并且每一种组合下 \(W(\bold x, z)\) 的值都不一样。如果我们能够证明： \[ \mathbb E_{x_z=y}(W(\bold x, z)) = \frac{1}{p_{SIR}(y)} \] 就相当于将估计式变成了蒙特卡洛估计，结果自然是无偏的。

至于为何期望能拿来替换pdf，我觉得可以感性理解，也许不是太严谨，Understanding The Math Behind ReStir DI 给出了证明。

继续证明，用类似描述SIRPDF的思路写出上面这个 \(\mathbb E\)： \[ \mathbb E_{x_z=y}(W(\bold x, z)) = \sum_{i\in Z(y)} \int_{\bold x| x_i=y} W(\bold x, i) \frac{p(\bold x,i)}{p_{SIR}(y)} d\bold x \] 这是一个条件期望，上式中，\(p(\bold x,i)\) 是采样到这样一个样本集，并重采样到index \(i\) 的概率，还需 要除以 \(p_{SIR}(y)\) 才是已知结果为 \(y\) 时的条件概率。继续展开： $$ \[\begin{align*} \mathbb E_{x_z=y}(W(\bold x, z)) &= \frac{1}{p_{SIR}(y)} \sum_{i\in Z(y)} \int_{\bold x| x_i=y} \left[\frac{1}{\hat p(x_i)} \frac{\sum_{j=1}^M w_j(x_j) }{M} \right] \left[ \frac{w_i(x_i)}{\sum_{j=1}^M w_j(x_j)} \prod_{j=1}^M p_j(x_j) \right] d\bold x \\ &= \frac{1}{p_{SIR}(y)} \sum_{i\in Z(y)} \int_{\bold x| x_i=y} \frac{w_i(x_i)}{\hat p(x_i)M} \prod_{j=1}^M p_j(x_j) d\bold x \\ &= \frac{1}{p_{SIR}(y)}\frac{1}{M} \sum_{i\in Z(y)} \int_{\bold x| x_i=y} \frac{1}{p(x_i)} \prod_{j=1}^M p_j(x_j) d\bold x \\ &= \frac{1}{p_{SIR}(y)} \frac{1}{M} \sum_{i\in Z(y)} \int_{\bold x| x_i=y} \prod_{x_j \in \bold x-x_i } p_j(x_j) d\bold x \\ &= \frac{1}{p_{SIR}(y)} \frac{Z(y)}{M} \end{align*}\] $$ 最后一步，被积项即为 \(\{\bold x |x_i=y\}\) 中所有样本集的出现概率的积分，即为1。

于是，当 \(Z(y)=M\) 时，\(W(\bold x, z)\) 的期望为 \(1/p_{SIR}(x_z)\)，估计是无偏的。

实际情况中，若提议分布并不能保证处处 \(>0\)，则估计是有偏的。我们可以修改： \[ W(\bold x,z) = \frac{1}{\hat p(x_z)}\frac{\sum_{j=1}^M w_j(x_j) }{Z(x_z)} \] 达成无偏。不过这样并不是最好的，可以使用类似MIS的方式加权： \[ W(\bold x,z) = \frac{1}{\hat p(x_z)} m_z(x_z)\sum_{j=1}^M w_j(x_j) \] 满足 \(\sum_i^M m_i(x) = 1\) 对于任意 \(x\) 均成立即可，一种启发式平衡策略为 \(m_i(x) = \frac{p_i(x)}{\sum_{j=1}^M p_j(x)}\)

可以将该式代入上面的证明过程，很容易证明。

总结一下，这一节我们证明了 \(\mathbb E_{x_z=y}(W(\bold x, z)) = \frac{1}{p_{SIR}(x_z)}\)，可以在估计中使用 \(W\) 替代 \(p_{SIR}\) 的作用。另外还还说明了RIS支持使用不同的提议分布。

加权蓄水池采样（WRS）

考虑流式地处理提议样本，即已有 \(M\) 个提议样本 \(x_1,..x_M\) 和SIR样本 \(y\)（可以为 \(N\) 个重采样样本，此处仅考虑一个的情况），现需要加入第 \(M+1\) 个提议样本 \(x_{M+1}\)，要维护SIR样本的概率正确。

用 \(w_{sum}\) 来表示此前 \(M\) 个样本的权重和 \(\sum w_i\)，\(w_{M+1}\) 可以直接算，那么样本 \(x_{M+1}\) 被采样的概率理应为 \(\frac{w_{M+1}}{w_{sum}+w_{M+1}}\)

此前所有样本 \(x_j,j\le M\) 被采样到的概率应当变为原来的 \(\frac{w_{sum}}{w_{sum}+w_{M+1}}\) 倍。

那么，策略就是以 \(\frac{w_{M+1}}{w_{sum}+w_{M+1}}\) 的概率替换原样本 \(y\) 。

WRS还支持两个蓄水池的合并：

\(w_{sum1}, y_1\) 合并 \(w_{sum2}, y_2\)，则 \(y_2\) 以 \(\frac{w_{sum2}}{w_{sum1} +w_{sum2}}\) 的概率替换 \(y_1\)，证明比较简单。

注意合并的时候维护 \(w_{sum}\)

不同目标分布的蓄水池合并

在上面，我们已经证明了RIS可以使用各不相同的提议分布，现在利用这一点，实现两个连目标分布都不同的蓄水池合并。这也是所有时空复用的基础。

首先，这种策略仅适合两个蓄水池的目标分布接近的情况（相邻像素或相邻帧），若相差较远，此方法同样是无偏的，但合并不会让采样质量更高。

以合并相邻像素的蓄水池为例，设当前像素为 \(q\)，蓄水池为 \(s\)，待合并像素为 \(q'\)，蓄水池为 \(r\)，蓄水池各自存储了 \(\left< w_{sum},y,M,W\right>\)，两个蓄水池中的目标分布 \(\hat p_q\) 和 \(\hat p_q'\) 不同，无法直接合并。

事实上，我们可以将相邻蓄水池的SIRPDF视为一个高质量的提议分布，\(r.y\) 即为该SIRPDF的一个样本，要将其加入 \(s\)，这就比较容易了。

下面是 Understanding The Math Behind ReStir DI 中给出的图。

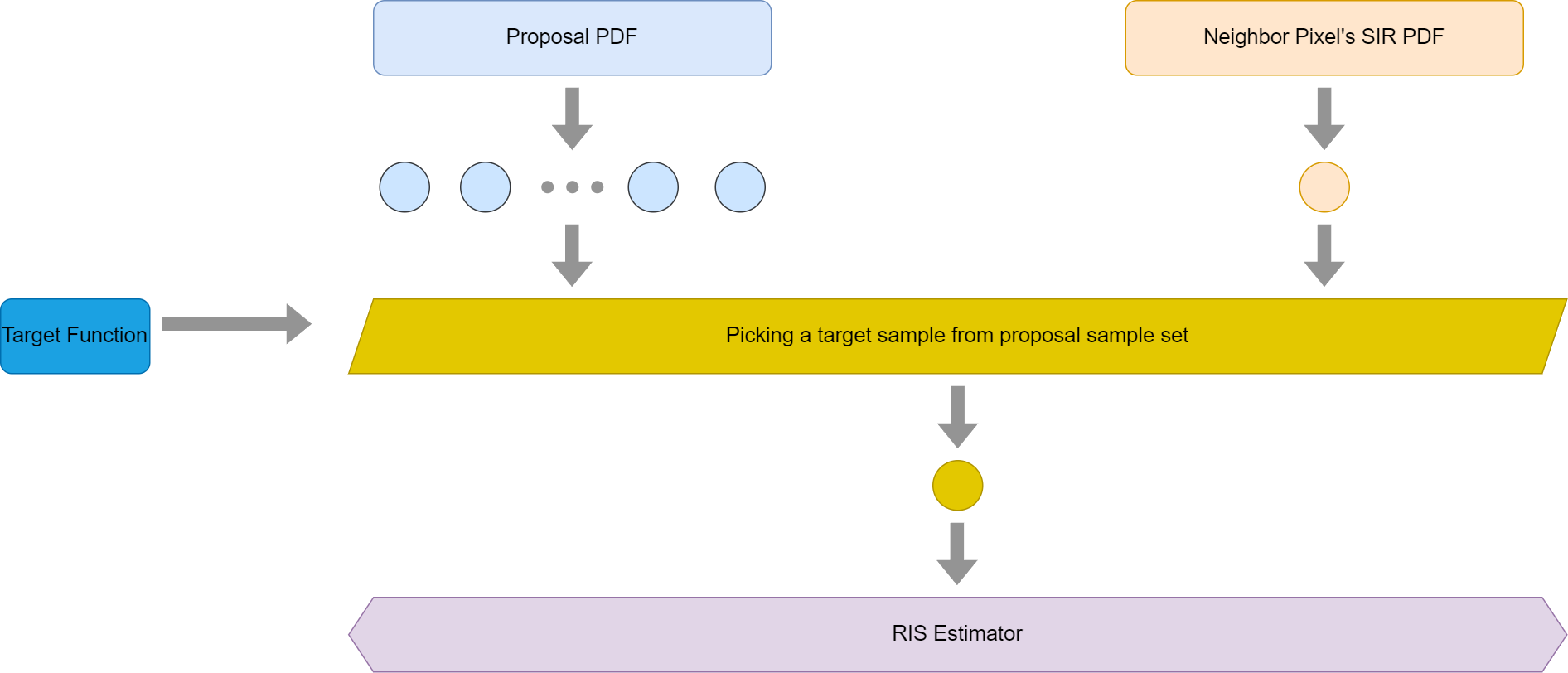
我们在先前已经证明了提议分布可以各不相同，且有了一个 \(W\) 用于代替 \(p_{SIR}\) 的作用。

要加入的样本权重为： \[ w = \frac{\hat p_q(r.y)}{p_{SIR}(r.y)} \Rarr \hat p_q(r.y) r.W = \frac{\hat p_q(r.y)}{\hat p_q'(r.y)} \frac{r.w_{sum}}{r.M} \] 中间再次利用了 \(W\) 的期望和 \(p_{SIR}\) 的关系，故没有写等号。

扩大SIR样本的影响

容易想到，\(r.y\) 应当是一个质量非常高的样本，代表了相邻像素的 \(r.M\) 个样本，仅仅将其视为一个提议样本有些浪费。考虑到它的重要程度和 \(r.M\) 相关，我们可以视为这个样本插入了 \(r.M\) 次，等价于插入一次，但权重乘了 \(r.M\) 倍（如果不理解为什么等价，可以算一下全部插入之后，\(r.y\) 替代上位的概率）。

于是最终的权重为： \[ \frac{\hat p_q(r.y)}{\hat p_q'(r.y)} r.w_{sum} \] 同样，\(s.M\) 也需要加上 \(r.M\)，而不是简单地+1。

这种权重也可以理解为一种MIS，不过由于后面计算 \(Z(y)\) 时还用到了这种思想，我更倾向于将其理解为插入 \(M\) 次，私以为更加容易理解。

注意：这种重用和真的把 \(s.M+r.M\) 个样本拿来重采样一次是不等价的，但同样能反映采样质量随着提议样本数 \(M\) 的提高而提高。

ReSTIR DI

最关键的蓄水池合并问题已经解决了，空间样本重用方法见上，时域样本重用也只是合并来自上一帧的蓄水池，寻找上一帧的对应也是利用Motion Vector。

TAA是有偏的，我们需要头疼上一帧和这一帧在各种情况下的不同，并且通常很难做到尽善尽美。而ReSTIR的时域重用是无偏的，因为我们的重用策略本身就支持合并目标分布不同的蓄水池，将另一个蓄水池并过来后，仍然是对当前目标分布的无偏估计，可以放心大胆的合并。

可见性重用

ReSTIR DI的目标分布是去掉可见性项后的直接光照 \(\rho L_eG\)，这样的好处是在计算 \(\hat p\) 时无需进行场景求交，但这也带来了一定的噪声。

Understanding The Math Behind ReStir DI 指出的方案是在目标分布中带上可见性项，这里似乎和原文的思路不同。原文将其策略称为Visibility Reuse，并没有提及要改变目标分布，下面按照原文的思路来：

原文方法非常简单：在蓄水池合并时，检测SIR样本 \(y\) 是否可见，若不可见，则直接将该蓄水池的 \(W\) 设为0，相当于丢弃了这一蓄水池。这阻止了被遮挡的样本向外传播，使得最终使用的样本大概率是不被遮挡的。

无偏版本实现

回忆一下，无偏版本需要修改 \(W\)： \[ W(\bold x,z) = \frac{1}{\hat p(y)}\frac{\sum_{j=1}^M w_j(x_j) }{Z(y)}, y=x_z \]

考虑如何计算这个 \(Z(y)\)，它表示 \(M\) 个样本（来自于 \(M\) 个提议分布）中，有多少提议分布满足 \(p_i(y) > 0\)。

有两个问题：1. 提议分布可能来自相邻的SIRPDF，它没有闭合解；2. 我们不可能追踪所有Proposal PDF。

对于第一个问题，由于 \(\hat p(x)\) 与SIRPDF在同样的区域成为0（参照SIRPDF的定义式），可以用 \(\hat p(x)\) 来代替SIRPDF来计算 \(Z\)。

对于第二个问题，我们需要再次强调插入 \(M\) 次的思想：在合并一个蓄水池 \(r\) 的时候，我们并不是合并这个蓄水池的所有历史样本，而是视为当前的SIRPDF样本 \(r.y\) 插入了 \(r.M\) 次，这 \(r.M\) 个样本全部来自于该SIRPDF。于是只要 \(p_{SIR}(y) > 0\)，就可以直接令 \(Z += r.M\) 。

计算过程可以看论文中的伪代码。

至于MIS版本的 \(W\)： \[ W(\bold x,z) = \frac{1}{\hat p(x_z)} \frac{p_z(x_z)}{\sum_{j=1}^M p_j(x_z)} \sum_{j=1}^M w_j(x_j) \] 这个版本的无偏公式在论文中没有实现，我也不知道具体要怎么实现。

Problem

• 为什么去掉可见性项，计算 $p $ 就不需要光线求交了？如何从给定位置+方向找到光源？