BXDF以及MR工作流

基本物理观念

1. 金属的折射光会被自由电子立刻吸收，几乎只有反射。非金属才有明显散射行为。
2. 非金属的镜面反射是无彩色的（白色），金属才具有彩色的镜面反射。
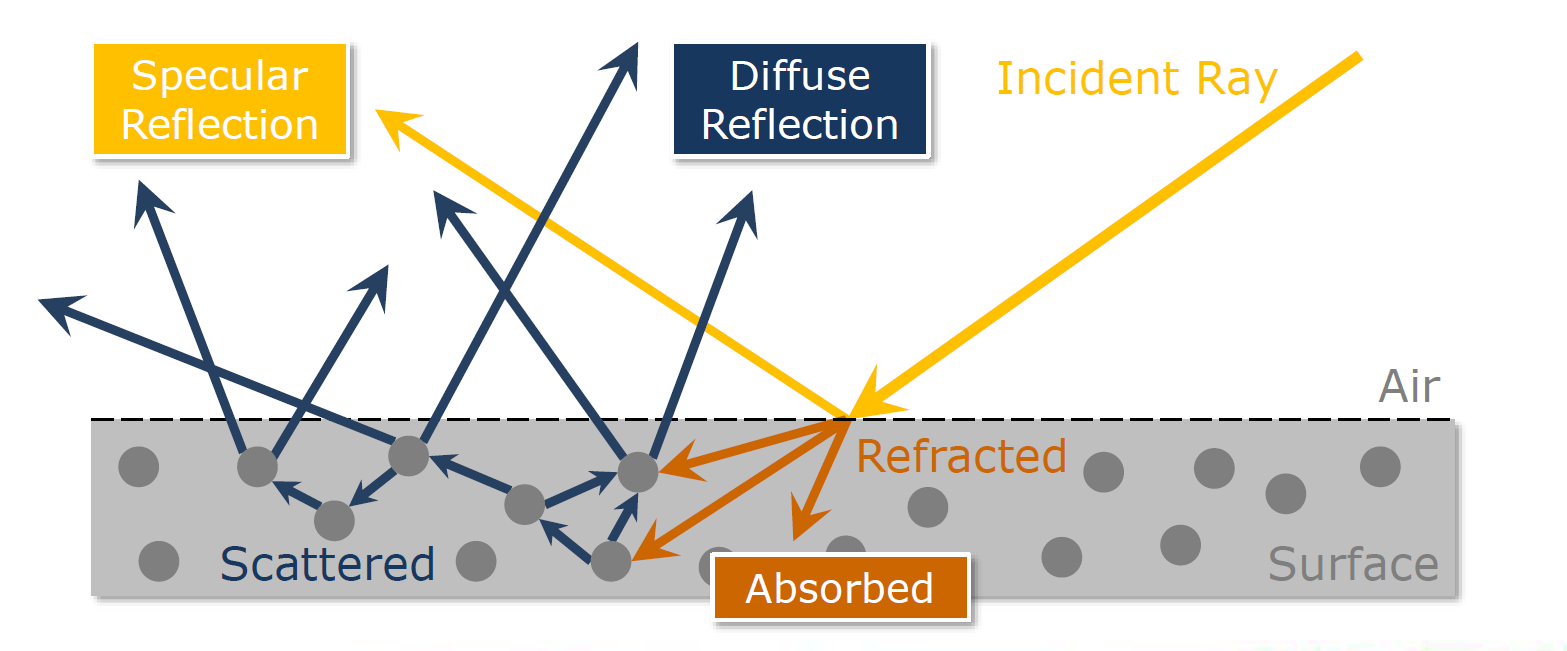
3. 光打中平面后，只发生反射（镜面反射）和折射，折射入物体内部后一部分被吸收，另一部分散射出来成为漫反射。其中漫反射部分又可以拆分出次表面散射，即散射距离显著大于像素大小时，散射影响到了附件的其他像素上，称为次表面散射。

BRDF

定义

BRDF的定义式：
$$
f_r = \frac{dL_o}{d E_i}
$$
此前我疑惑过为什么不简单定义为 $\frac{dL_o}{d L_i}$，在搞明白Radiance之后理解了。$L_o$ 为反射方向的Radiance，贡献来自于整个上半球，$dL_o$ 指 $dw_i$ 方向的入射光对 $L_o$ 的贡献；$E$ 为表面接受到Irradiance，贡献来自于整个上半球， $dE_i$ 指 $dw_i$ 方向的入射光对 $E$ 的贡献。

简单而言，他们都是微分量，都是对入射角的微分；而 $dL_i$ 则说不清具体含义；也不可能定义成 $\frac{dL_o}{L_i}$ 的形式，它是一个趋于0的值，需要除上一个微分立体角才能有意义。

$$
L_o = L_i \cdot f_r(i,o)\cdot cos(i) \
L_i = L_o \cdot f_r(o,i)\cdot cos(o)
$$

那为什么不定义为 $\frac{dL_o}{L_i dw_i}$ 的形式呢？（相比正式定义少了个 $cos$）

还可以从实际测量的角度理解，实际测量中 $dL_o$

….

除此之外，在最常见的微表面模型中，这种定义的BRDF是可逆的，带上cos之后就不可逆了。

Microfacet BRDF推导

下面推导微表面模型中的 $f_r$ 具体形式，暂时忽略菲涅尔项和几何遮蔽。

我们用 $cos(i,n)$ 这样的形式来表示两向量夹角的 $cos$。

设 $D(h)$ 指代微法线在 $dw_h$ 微立体角内的微表面面积与宏表面面积的比例，有
$$
\int D(h) \cdot cos(n,h) \cdot dw_h = 1
$$
先推导 $dL_o$，它指 $dw_i$ 方向的入射光对 $L_o$ 的贡献。

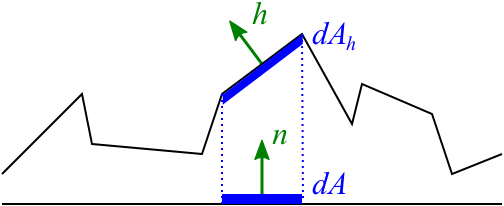
首先，$dw_h$ 方向的微表面面积为
$$
d^2A_h = dA \cdot D(h) \cdot dw_h
$$
可以得出进入表面（且对 $L_o$ 有贡献）的辐射通量（微平面视角下理解）：
$$
d^3\phi = L_i \cdot d^2A_h \cdot dw_i \cdot cos(h,i)
$$
$\phi$ 是由输入到输出的不变量 $\phi_i=\phi_o$，那么可以得到（回到宏观视角）：
$$
dL_o = \frac{d^3\phi}{dA\cdot dw_o \cdot cos(n,o)}
$$
左侧是 $dL_o$，因为右侧还是对 $dw_i$ 微分的一个量，得到的正是 $dw_i$ 方向对 $L_o$ 的贡献。也可以从 $d$ 的次数守恒来理解。

$dE_i$ 比较简单：
$$
E_i = \int L_i \cdot cos(n,i) \cdot dw_i \
dE_i = L_i \cdot cos(n,i) \cdot dw_i
$$
那么展开上述式子，得到：
$$
f_r = \frac{D(h) \cdot cos(h,i) \cdot dw_h}{cos(n,o) \cdot cos(n, i) \cdot dw_o}
$$
$dw_h$ 与 $dw_o$ 之间存在一个几何上的关系

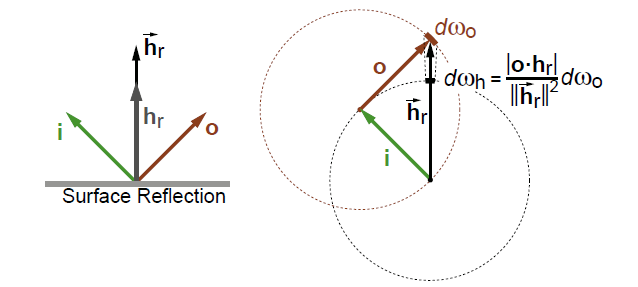
这是Walter 07年论文中的图，很多博客也喜欢从这张图出发解释它们的几何关系，但由于我个人无法理解这个图的作图逻辑，所以从另一个角度来解释。

首先，显然有 $d_{\theta o} = 2d_{\theta h}$，$d_{\phi o} = 2d_{\phi h}$

从立体角定义的角度，$dw_h = d_{\theta h} d_{\phi h}cos(\theta_h)$，我们将 $h$ 摆到竖直的位置上，就有了
$$
dw_h = d_{\theta h} d_{\phi h} \
dw_o = d_{\theta o} d_{\phi o} |w_o\cdot w_h| = 4|w_o\cdot w_h|dw_h
$$
于是有：
$$
f_r = \frac{D(h)}{4cos(n,i) \cdot cos(n,o)}
$$

再加上几何项G与菲涅尔项F，就得到了经典的Cook-Torrance BRDF 形式：
$$
f_r=\frac{DFG}{4cos(n,i) \cdot cos(n,o)}
$$
当然，这里只考虑了reflect，通常的反射模型还要再加一个diffuse部分。

可逆性：$f_r(w_r\rightarrow w_i)=f_r(w_i\rightarrow w_r)$

能量守恒：总量可以衰减（吸收），但不能多，这决定了光线追踪是否能够收敛（物理上的正确性）。

Diffuse

• 最简单的Lambert均匀漫反射：$f_{lambert}=\frac{q}{\pi}$

因为需要能量守恒：
$$
\int_{\Omega^+} f_p cos\theta d_w = 1
$$
得 $f_p = \frac{1}{\pi}$，再加上albedo系数即可。

• Disney经验模型，在漫反射部分也加上了菲涅尔因子，公式如下：

$$
f_d = \frac{baseColor}{\pi}(1+(F_{D90} - 1)(1 - cos_{NL})^5)(1+(F_{D90} - 1)(1 - cos_{NV})^5)\
F_{D90} = 0.5 + 2roughness \times cos_{VH}^2
$$

• 次表面散射也属于Diffuse，暂略。

D项

$D(h)$ 指微表面中法线为 $h$ 的微表面面积比例，是微表面模型中最重要的一个统计量。

它指的是微表面面积 / 宏观面积，故乘上余弦项后积分才为1。
$$
\int_{\Omega^+} D(h)(h\cdot n)dw_h = 1\
\int_{\Omega^+} D(h)(h\cdot v)dw_h = v\cdot n
$$
关于2式的理解：

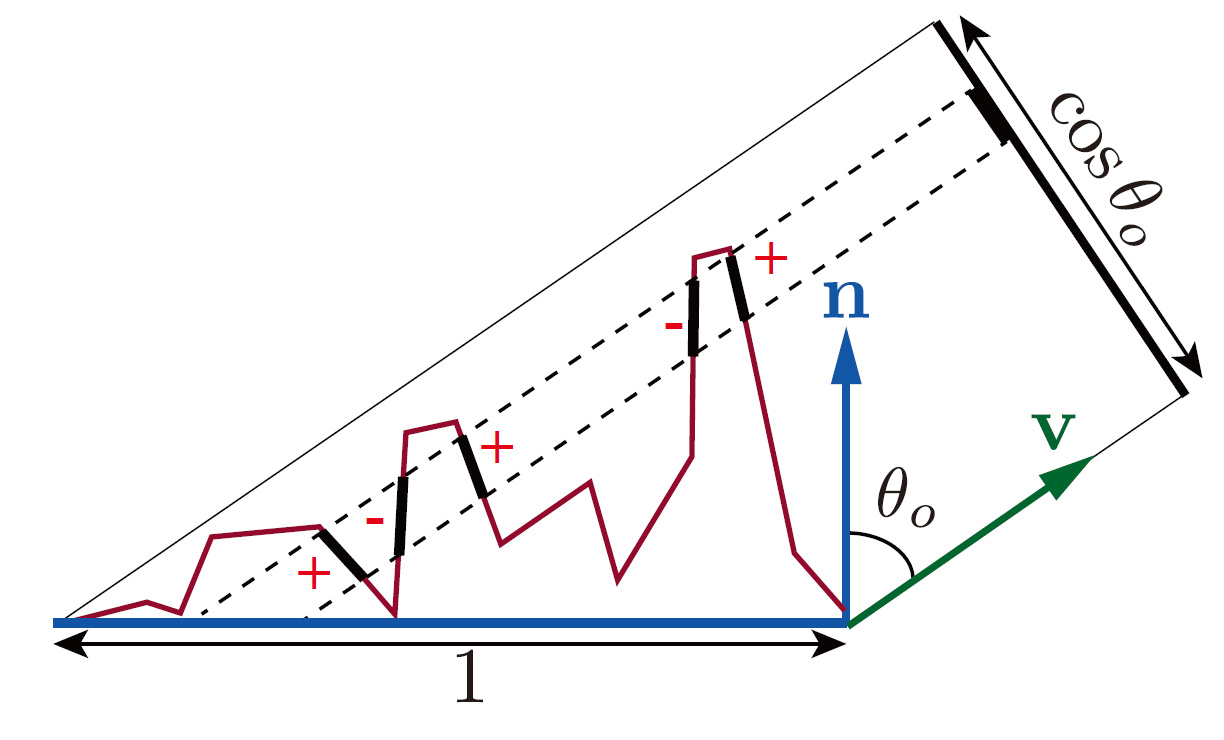
比较常用各项同性GGX分布：
$$
D_{GGX}(h)=\frac{\alpha^2}{\pi(cos_{NH}^2(\alpha^2-1)+1)^2}
$$

式子中 $\alpha$ 表示粗糙度 roughness ，其值越大，反射越不集中。

除此之外还有许多中分布模型，大多公式不是推导出来的，而是凭借经验和直觉拟合测量结果得出的。

形状不变性：缩放 $\alpha$ 时，等价于拉伸微观几何。GGX具备形状不变性，而另一个常见的GTR模型不具备。

各向异性：暂略

G项

几何项，微表面模型中，一部分微表面会被遮挡，导致即使其法线方向符合，也没有产生贡献。我们用 $G1(h,v)$ 表示沿视图 $v$ 方向，可见的法线为 $h$ 的微平面比例，作为对 $D$ 项的补充。

之前的 $D$ 项、漫反射项的常用分布，都是人们依据经验拟合的，而G项是依赖所选D项，可以推导的。

单D项还不能推导出G，因为D项仅定义了分布，未定义“轮廓”，还需要一个定义轮廓的模型。目前最好的轮廓模型是Smith遮蔽函数。

Smith遮蔽函数的具体内容暂略（（（（

Smith模型将微表面看做若干不连续的表面（无自相关性，即轮廓不连续），这当然与现实不符，不过在表面随机的情况下表现很好，对于具备一定规律的表面材质，一般使用专门的模型。

Smith遮蔽函数是常见遮蔽函数中，唯一既满足能量守恒又具有法线遮蔽独立性（即法线/高度都和相邻点无关）便利特性的函数。

下面是GGX导出的G项：Smith-GGX函数
$$
G_{GGX}(v)=\frac{2(n\cdot v)}{(n\cdot v)+\sqrt{a^2+(1-a^2)(n\cdot v)^2}}
$$

其中 $v$ 为光线方向，显然角度越大，这个项越小（衰减越重）

其中 $\alpha=(\frac{1+roughness}{2})^2$，也有其他形式的 $\alpha$。

我们要用的几何项同时考虑入射和出射方向的几何遮蔽，$G=G_{GGX}(w_i) G_{GGX}(w_o)$

G项虽然基本都用Smith，但是有很多不同的近似方案，内容较多，具体见https://github.com/QianMo/PBR-White-Paper/blob/master/content/part%205/README.md

Kulla-Conty近似：

简单地乘以G项显然会导致能量丢失，事实上，被遮挡的部分会经过反弹再出去。

这里需要做一个fix【暂略】

不能单纯加上一个diffuse！

F项

菲涅尔项，指物体镜面反射的能量比例，入射角与法线夹角越大，反射率越大。通常用 $F_0$ 表示0度角（垂直）入射时的反射率。金属的 $F_0$ 值通常为 $0.5-1$，非金属通常为 $0.02-0.05$。

在掠射（90度）时，菲涅尔项达到1（全反射），不过由于微表面的存在，宏观观察的菲涅尔项达不到1也很正常。

菲涅尔项的实际计算比较复杂，它与材质的折射率、波动光学相关，不同材质的菲涅尔项差别也很大。但是经过一些观察，人们发现了一些共性：

• 对于0-45度的入射角（与法线夹角），菲涅尔项几乎不变。
• 45-75度，菲涅尔项明显增大，75-90度，菲涅尔项总是快速达到1。

因此可以用 $F_0$ 来近似地确定整个菲涅尔函数。

一种近似求法 SchlickFresnel：
$$
F=F_0+(1-F_0)(1-cos\theta)^5
$$
$cos\theta$ 为入射方向与法线的夹角（$w_i\cdot h$），随角度增大逐渐拉到全部反射。

常见材质的 $F_0$ 可以查表得出，也可以用 $F_0=(\frac{n_1-n_2}{n_1+n_2})^2$ 来计算，这里看到 $F_0$ 其实并不是一个属于材质的属性，而是与两边介质的折射率均有关，大多数情况下 $n_1 = 1$。

在相对IOR接近1时，上述式子误差较大，此时可以直接使用精确菲涅尔方程计算。

据人们观察，非金属的菲涅尔效应在光的各个波长上表现比较一致，而金属的菲涅尔效应随波长变化明显。因此实现上，金属的F0可以定义为彩色，非金属F0定义为白色，混合介质的 $F_0$ 可以简单地线性估计：F_0=mix(vec3(0.04), albedo, metallic)，这个式子中，非金属F0取典型值0.04，金属部分F0 = albedo，这也是M/R工作流中的常见做法，albedo同时作为非金属的漫反射颜色和金属的F0。

菲涅尔项是可逆的（仅限目前的几何光学），就是说 $F(w_i, w_o)=F(w_o, w_i)$，这一点无论是反射还是折射都成立。

Disney模型

Disney BRDF将物体视为金属部分和非金属部分，依据金属度 metallic 混合。由于仅非金属具有漫反射，我们为diffuse部分乘一个系数 $(1-metallic)$，右部specular为金属和非金属共同作用的，金属度体现在 $F$ 项中的 $F_0 = mix(0.04, albedo, metallic)$。

漫反射属于折射后的散射，理应也具有与菲涅尔相关的系数，Disney没有使用简单的lambert模型也没有乘（1-F），而是单独加了一些菲涅尔因子（具体见上Diffuse）

$$
f_r = (1 - metallic)f_d + \frac{D_{GGX}F_{SchlickFresnel}G_{SchlickGGX}}{4cos_i cos_o}
$$

BSDF

BSDF = BRDF + BTDF

BTDF（双向透射分布函数）的积分域是下半球面，与BRDF组合后就是一个完整的球面积分。

BTDF同样可以使用微表面模型，将微表面看做光滑的，只会朝固定方向折射。

那么BTDF前面的推导过程和BRDF完全一致，得到：
$$
f_t = \frac{D(h) \cdot cos(h,i) \cdot dw_h}{cos(n,o) \cdot cos(n, i) \cdot dw_o}
$$
最后的 $\frac{dw_h}{dw_o}$ 和BRDF不同（仅仅是几何关系上不同），见Walter论文中的图，可以推出关系：
$$
dw_h = \frac{dw_o \cdot \eta^2 \cdot cos(h,o)}{||h||^2}
$$
这里的 $\eta = \frac{\eta_o}{\eta_i}$，合并起来，得到 $f_t$ 的表达式：
$$
f_t =\frac{cos(h,i) \cdot cos(h,o)}{cos(n,o) \cdot cos(n, i)}\cdot \frac{D(h) \cdot \eta^2}{||h||^2}
$$
再添加菲涅尔项（1-F）和几何项，定义都与BRDF中一致。

由于折射两边的介质不同，我们发现这个式子并不是可逆的，但幸运的是还有另一种可逆性存在：
$$
f_t(i,o) \cdot \eta_i^2 = f_t(o,i) \cdot \eta_o^2
$$

Disney BSDF

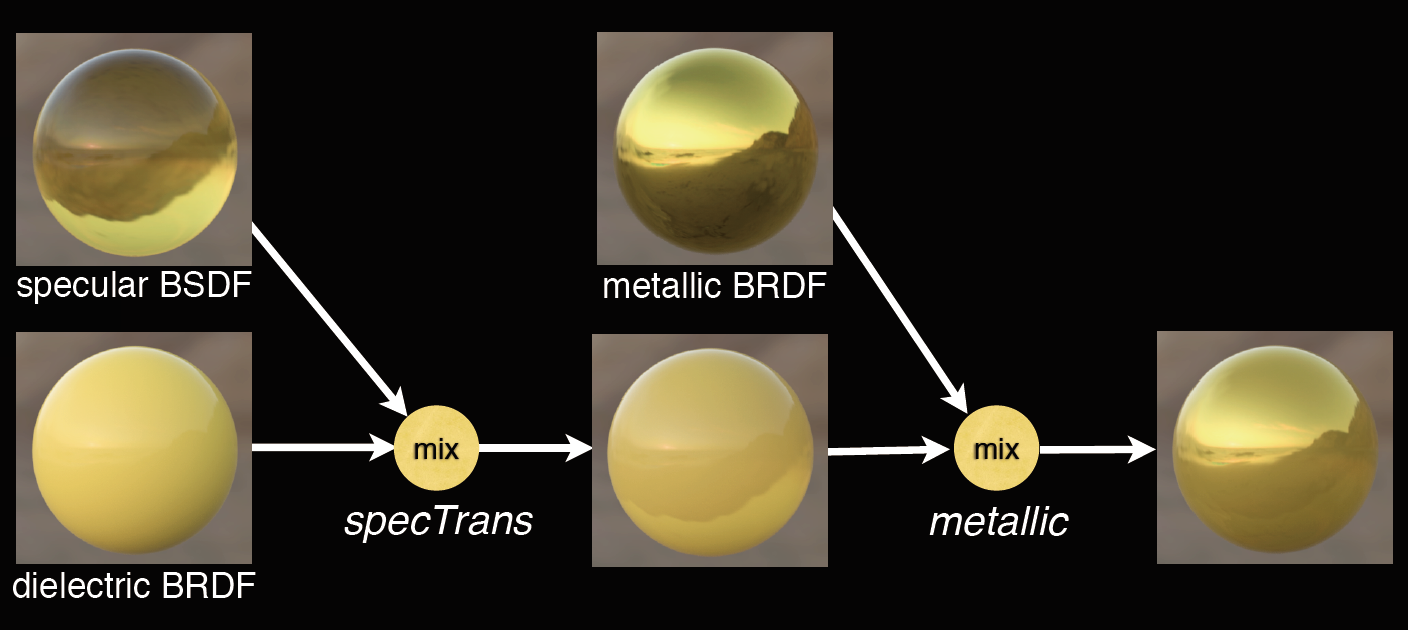
原先的BRDF依据metallic划分为了散射和反射两部分，现在继续在散射中划分为折射（Specular BSDF）和漫反射两部分（Disney方法使用specTrans参数）。

折射部分和反射很接近，只不过菲涅尔项需要使用 $1-F$ 以及 $IOR$ 修正，此时的菲涅尔项可以直接用折射率算出来精确值。

折射下的半法向：$h=normalize(wi+\frac{\eta_2}{\eta_1}wo)$

它的分布 $D(h)$ 可以按照和BRDF相同的方式得出。

实际应用中，我们通常以表面法线朝向作为外侧，定义介质内外两侧的折射率（外侧通常视为空气）

重要性采样

对D进行重要性采样

我们很难严格画出渲染方程的曲线，故通常只对法线分布函数进行重要性采样。

如上，$D(h)$ 实际应满足 $\int_{\Omega^+} D(h)cos\theta_hd_w=1$，$\theta_h$ 为宏面法线和 $h$ 的夹角，那太方便了，直接拿 $D(h)cos\theta_h$ 当概率密度，采样 $h$。

将向量转化到球面坐标系 $\theta,\phi$：
$$
\int_0^{2\pi}\int_0^{\pi} D(\theta, \phi) cos_\theta sin_\theta d_{\theta}d_{\phi}
$$
显然这里的式子与 $\phi$ 无关，我们可以得到 $pdf(\theta)=\frac{2\alpha^2cos\theta sin\theta}{(cos^2\theta(\alpha^2-1)+1)^2}$

接下来的问题是如何生成一个符合这个概率的随机数：

逆分布函数方法

首先计算 $pdf(x)$ 的累计分布函数 $P(x)$，它的值域是 $[0, 1]$，然后利用反函数 $P^{-1}(x)$ 。

这样就可以利用 $[0,1]$ 之间的均匀随机数生成符合 $pdf(x)$ 的随机数。

为了方便起见，设 $x=cos\theta$
$$
\begin{aligned}
p(\theta)=&\frac{2\alpha^2cos\theta sin\theta}{(x^2(\alpha^2-1)+1)^2}, x\in[0,1]\
P(t)=&\int_0^t\frac{2\alpha^2cos\theta sin\theta}{(x^2(\alpha^2-1)+1)^2}d\theta\
=&\int_{..}\frac{\alpha^2}{(x^2(\alpha^2-1)+1)^2}dx^2\
=&\int_{..}\frac{a^2}{u^2(a^2-1)}du,u=x^2(a^2-1)\
=&\frac{a^2}{(a^2-1)(cos^2t(a^2-1)+1)}-\frac{1}{a^2-1}\
P^{-1}(x)=&\arccos\sqrt \frac{1-x}{x(a^2-1)+1}
\end{aligned}
$$
故随机抽样 $x\in [0,1]$，然后得出 $\theta=P^{-1}(x)$。$\phi$ 这一项是均匀的， 在 $[0,2\pi]$ 上随机即可。注意pdf还需除以这个 $2\pi$

注意如此采样的是 $h$，随后可以进行反射得到 $wo$ 方向，此时还需要再次应用 $wh,wo$ 之间的变换比例：$pdf /= 4cos_{ih}$。

对环境贴图重要性采样

以HDR环境贴图作为主要光源时，对其进行重要性采样。

首先将HDR贴图的颜色值归一化为概率密度

此时我们相当于有了一个函数 $pdf(x, y)$​，只不过没有解析式，求不出cdf，那就只能二分了。

可以求出边缘密度函数 $F_x(x)=F(x,\infty)$，它相当于前缀和，我们可以在[0,1]间均匀抽样，然后在 $F_x$ 上面二分得到采样的 $x$

然后在 $x$ 列上求出每个 $y$ 的条件概率密度 $f_{Y|X}(y)$，在这个东西的CDF上同理二分得到 $y$。

在GPU中二分实在太慢，我们可以先预处理一个二维缓冲，在这个缓冲中以 $(u,v)$ 采样的值对应上述过程中，随机数为 $u,v$ 时采得的 $x,y$ 坐标。同时还需要传递这个位置的pdf，一共三个浮点数，正好利用三个通道。

显然这个cache和原图的关系基本上是“连续”的，被插值了也没有关系。

关于pdf：谨记它表示的是这个值被采样到的概率，而非此次采样发生的概率，不可忽略。