光线追踪入门

光线与平面求交

光线可以表示为 $r=o+td$，其中 $o$ 为原点，$d$ 为方向。

隐式表面

隐式表面定义为 $f(p)=0$

则求解 $f(o+td)=0$ 即可，取 $t$ 最小值（$t>0$）对应处作为交点。

显示表面

光线与三角形求交：

首先计算光线与三角形所在平面的交点，然后计算点是否在三角形内。

平面的方程：$f(p)=(p-p’)\cdot N=0$，$p’$ 为平面上任意点，$N$ 为平面的任意垂线，而从三角形得出这样的平面参数很简单。

另一种方式：列出三角形面的方程（重心坐标），得到 $O+tD=(1-u-v)P_0+uP_1+vP_2$，它可以写作一个线性方程组，解得 $t,u,v$，然后判断重心坐标是否都在 $[0,1]$ 内。

此处碰撞得到的 $u,v$ 可以记录下来，之后用这个坐标获取表面材质信息。

AABB

轴对齐包围盒（Axis-Aligened Bounding Box）

求光线与包围盒是否相交：包围盒有三个对面，计算光线与每对面相交的两个 $t$ 值（$t_{min}$ 和 $t_{max}$），得到三组 $t$ 的区间，这三组的区间的交集即为光线在盒子中的时间。

Grid方法

旧方法

将区域划分为很多个格子，计算每个格子中是否有物体，光线进入时可以采用类似Bresenham的方法计算接触的格子（很快），若格子中有物体再检测。

空间划分方法

八叉树

每次划分都划分为8块，直到区域不包含内容或者足够小

KD-Tree

每次仅将区域划分为2块，采用某种策略选取最优的划分位置和方向。

划分的方向还是平行的

中间节点都是包围盒，物体都存在叶子节点中。

一个图元可能被划分到多个空间中，此时这个图元就需要在多个空间中都进行求交。

BSP-Tree

在KD-tree的基础上，划分方向可以是斜的，划分效果可能更好，但抛弃了AABB，计算效率并不优秀。

BVH

Bounding Volume Hierarchy

基于物体的划分，而非基于空间的划分。

和KD-Tree差不多，但是划分时不再是将空间一刀划开，而是将其中物体分为两个部分，两个部分各自形成一棵子树，两个子树的包围盒可以重叠，这使得每个图元可以仅属于一棵子树。

实现起来非常容易，可以直接根据父包围盒三维的长度，在最长的一维上，按三角形个数划分（一半划到左一半划到右，$O(n)$ 找出中位数即可）。

递归求交时，严格意义上来说两个子空间是没有先后顺序的，即使在一个空间内找到了交点，另一个必须求交计算，这使得朴素BVH求交效率会低于kd-tree。我们很容易想到一些剪枝：根据包围盒的交点决定顺序，若在第一个空间中已经得到交点，且在第二个空间的包围盒交点之前，则跳过。

SAH优化

按三角形个数进行的划分有显而易见的问题，当出现特别大时三角形时，划分不那么均匀，重叠部分也可能非常大。

SAH (Surface Area Heuristic) 优化即按照包围表盒面积来确定一个最优的划分方案。粗略认为，一个包围盒被击中的概率与其面积成 $S$ 正比，而击中这个包围盒之后的开销，又可以粗略认为和其中的物体数 $N$ 成正比。于是SAH策略要求我们找到 $S_1N_1+S_2N_2$ 最小的划分策略。

需要排序，前后各扫一遍预处理出包围盒之后，尝试所有划分点即可（三个轴各自来一次）。

Radiometry

立体角

steradians

二维角度的标准定义（弧度）：$\theta=\frac{l}{r}$，弧长/半径

三维立体角的定义：$w = \frac{A}{r^2}$，弧面面积/半径方

单位立体角：

在球面上 $(\theta,\phi)$ （通常 $\theta$ 指与z轴的夹角，$\phi$ 指在xy平面上投影的经典一维角度）处，画图容易计算弧面的微分
$$
d_A=(rd_\theta)(rsin_\theta d_\phi)
$$
则有单位立体角（微分立体角）
$$
d_w=\frac{d_A}{r^2}=sin_\theta d_\theta d_\phi
$$
立体角积分：
$$
\theta\leq \pi,\phi\leq 2\pi\
\int_{\Omega^+}d_w=\int_0^{2\pi}\int_0^{\pi} sin_\theta d_\theta d_\phi=4\pi
$$

这里具体要看球面坐标怎么定义，知道原理即可。

辐射度量学

$\phi$：辐射通量，单位时间发出的能量 $\phi=\frac{dQ}{dt}$，类似功率。通量也可以理解为单位时间通过的光子数量。单位有流明 lumen

• 渲染中我们通常不会用到 $Q$，通常都是以 $\phi$ 来衡量能量。

$I$：Intensity，点光源发出的，在单位立体角上的Power，$I=\frac{d\phi}{dw}$，或 $I=\frac{\phi}{4\pi}$

$E$：Irradiance，每单位面积接受到的Power，$E=\frac{d\phi}{dA}$，这个量仅用来衡量单位面积上接收到的通量，并关心光是从什么方向入射的。

• 点光源自由发散时，随距离增大，Intensity不变（单位立体角上的光强没变），接受方的Irradiance按 $r^2$ 衰减。

$L$：Radiance，单位面积在单位立体角上的辐射Power $L=\frac{d^2\phi}{d_wd_Acos_\theta}$

• $E = \int_{\Omega^+} Lcos_\theta d_w$，这里看出，$E$ 是从表面角度来考虑的，而 $L$ 是从光线角度考虑的。

关于Radiance，我在很长一段时间里没能理解它的本质，从而对无法自己推导出BRDF的公式。另一件事情也同样困惑了我很久：直接光照下，光源距离物体越远，照明效果越差；而在路径追踪中，我们计算来自下一次反射的 $L_i$ 时，却根本不考虑下一个Bounce距离我们有多远。更进一步，人眼无论距离物体多远，看到的颜色都一样，应该怎么解释？

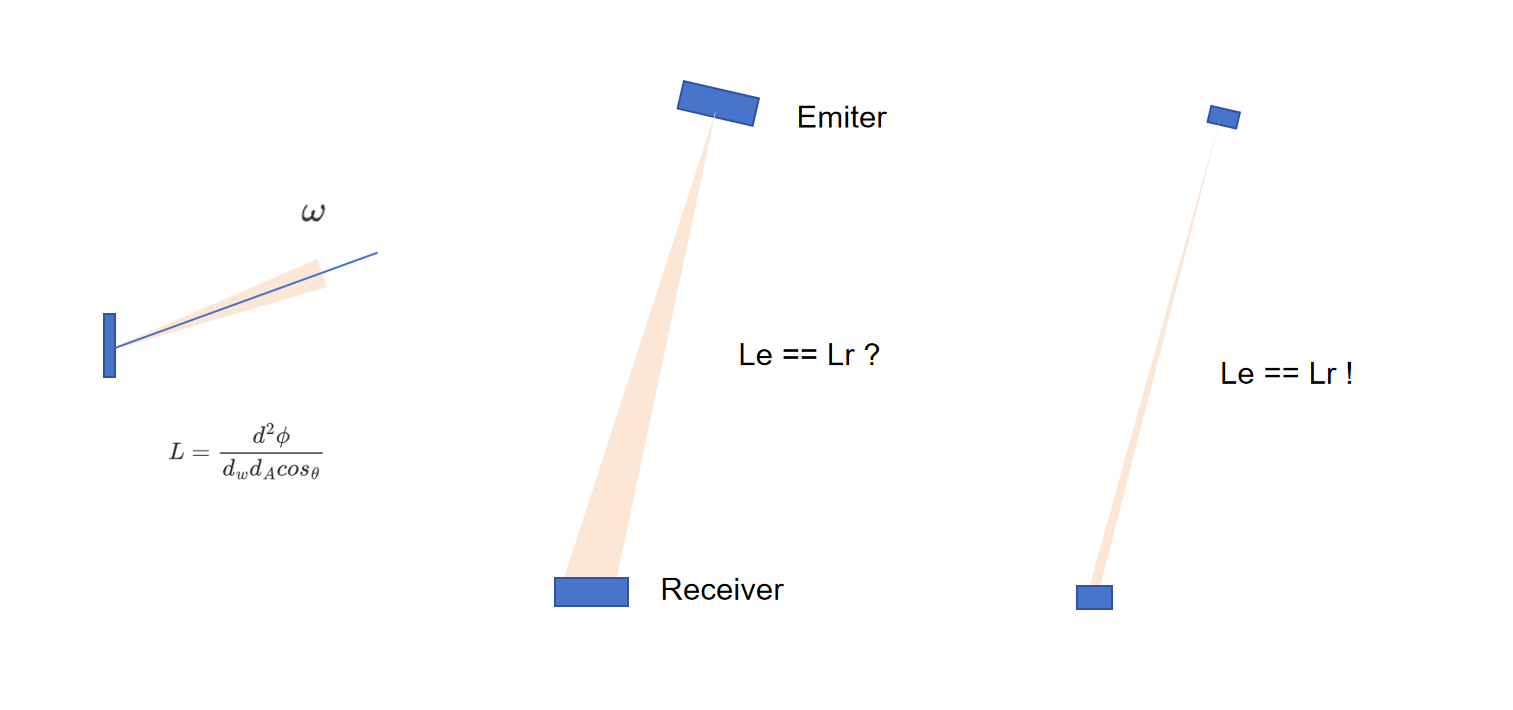
如果只看前两幅图，会觉得计算 $L_i$ 必然要考虑到双方之间的距离，并且处理起来很困难。同时还面临着“发射方的L和接收方的L是一个东西吗？”的疑问。

但当微分立体角无限小，$dA$ 无限小时，$L$ 就是一根光线（不存在近似，这是一个 $\frac{x}{\infty}$ 的问题）。它无论传输到近处还是远处，只要距离是有限的，都一样。

有了这个想法，一切都迎刃而解了：$L$ 是衡量光线的一个物理量，它不会随着传输距离而损耗。那么，发射方的Radiance和接收方的Radiance得以统一，Radiance成为了我们路径追踪中，最适合用于衡量光线能量的物理量。

人眼看到物体的颜色与距离无关，也可以用上述理论阐述：视网膜上任意微面 $dA$ 接收到的Radiance没有变，变了的只是物体在视网膜上成像的面积。

错误认识：物体发出很多根光线，随着距离增大，光线会变稀疏（Radiance变小）。

在 $d_w$ 无限细分的情况下，光线有无数根，在有限的距离下，Radiance不变。这是一个 $\frac{\infty}{x}$ 的问题。

渲染方程

$$
L_o(p,w_o)=L_e(p,w_o)+\int_{\Omega^+}L_i(p,w_i)f_r(p,w_i\rightarrow w_o)cos\theta_idw_i
$$
其中，$w$ 表示一个方向，$dw$ 为这个方向上的微分立体角。

$w_r$ 方向上的辐射，等于自身在这个方向的发光（辐射）加上所有其他方向 $w_i$ 入射的光反射对 $w_r$ 的贡献。$f_r(p,w_i\rightarrow w_r)$ 是一个BRDF方程，定义了一个方向的入射光对另一个方向出射光的贡献，通过定义不同的BRDF方程可以实现不同的材质。

渲染方程是递归定义的，是正确的，这里的正确指它完全符合现实世界，但我们实现时还是需要用到一点近似，或者说仅仅实现“期望上正确”。

蒙特卡洛方法

随机采样。

通用形式（使用任何分布的概率来采样），近似地求 $f(x)$ 的定积分，定积分域蕴含在随机变量 $X$ 中。
$$
\frac{1}{N}\sum_{i=1}^N \frac{f(X_i)}{p(X_i)}
$$
渲染方程应用蒙特卡洛方法之后（这里暂时忽略了自发光）：
$$
L_o(p,w_o)=\frac{1}{N}\sum_{i=1}^N \frac{L_i(p,w_i)f_r(p,w_i\rightarrow w_o)(n\cdot w_i)}{p(w_i)}
$$

注意：上式考虑到了 $X$ 的概率密度，故一定要按照 $X$ 的分布来抽样，而不能人为干预，否则结果的期望就不正确了。

多种策略下应用蒙特卡洛方法

采样蒙特卡洛方法可以使用任何分布的概率，都正确，而使用特殊的分布可以加速收敛（准确来说，能够降低采样结果的方差）。重要性采样即对贡献较大的方向以更高的概率采样。

还可以将直接光与间接光的贡献分开统计，但这里要注意期望的正确性，不能违背蒙特卡洛方法的概率性原则，否则会收敛于一个错误结果。

• 对于面积光源的采样，具体见下

• 对于点光源的采样，很麻烦，一般使用一个小面片代表点光源。

  • 一种错误的思路是直接加上点光源方向的贡献（设pdf=1），因为随机的间接光方向击中光源点的概率为0
  • 这种思路下，点光源距离物体的距离不影响点光源的贡献，显然是错误的。根本在于点光源在半球上的占比没有随着距离的增大而缩小。

• 对于环境光源，一种想法是将其单纯作为背景色，另一种策略是对其进行重要性采样，某种意义上相当于对直接光照单独考虑。

蒙特卡洛方法的要求

虽然概率分布可以随意，但也要注意一点：

• 所有 $f(x)\gt 0$ 的地方，需要有 $p(x)\gt 0$。
  • （我并没有找到这个定义，但自己想想是显然的）

可以随便举个极端例子，如只在前半段有概率，后半段无，那么结果的期望当然是不正确的。这本质是因为出现了未定义的 $\frac{0}{0}$，被当做了0处理。

不过，在 $f(x)=0$ 的地方，是可以有 $p(x)=0$ 的。

路径追踪

问题：即使随机采样，还是会出现指数爆炸的问题

• N = 1，仅反射一次，这样得到的图像会有大量噪声。
  • 每个像素发出多根光线以平均
  • 后期去噪

问题：无限递归

• 当然可以简单设置反弹次数，但不够好
• 轮盘赌法：设置一个概率 $p$，以概率 $p$ 往外反弹一次，得到的结果再除以 $p$，这样可以维护期望不变，场景亮度是真实的。

优化：直接光照、间接光照划分

• 思路：将直接光照和间接光照分开计算（分别划分到球面上的一块区域，各应用用蒙特卡洛方式积分）

• 因直接光照贡献较大，随机一条直线很可能碰不到直接光，故单独计算。

  • 面光源：在立体角上的采样改为在光源面上的采样。我们将光源面投影到立体角，得到映射关系 $dw = \frac{cos\theta’}{|x’-p|^2}dA$，其中 $x’$ 是在光源面上的抽样，$\theta’$ 是 $xx’$ 连线与光源面法线的夹角，直接光照的贡献为：
    $$
    L_o’=AL_i(p,w_i)f_r(p,w_i\rightarrow w_o)cos\theta\frac{cos\theta’}{|x’-x|^2}
    $$

  • 这是在光源面上均匀抽样了一个点，概率为 $1/A$，然后将对 $w$ 的积分改为对 $A$ 的积分。可以发现，这里实际上还蕴含了 $r^2$ 的距离衰减。

  • $xx’$ 连线若中间撞到其他物体，则直接光贡献为0

  • 点光源很难处理，一般可以使用微小的面光源代替

• 计算间接光照，若随机到的方向撞上了光源，则贡献为0

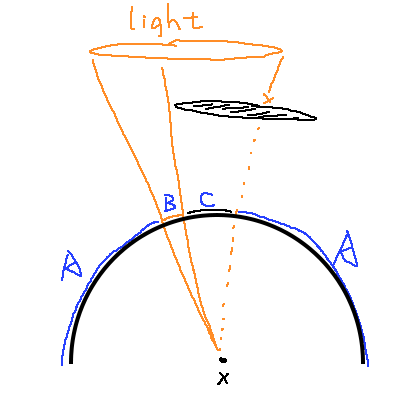
这里我将球面看做ABC三部分，直接光照求B+C段的蒙特卡洛积分，但将C段贡献视为0；间接光照求A+B+C段的蒙特卡洛积分，但将B段贡献视为0，故直接光照与间接光照相加，恰好为整个球面上的积分。至此，路径追踪仍然保持了期望上的正确性。

这种每个交点都求一次直接光照贡献的方法其实就是所谓的NEE (Next Event Estimation)。

调试策略

单纯的蒙特卡洛方法无疑是正确的，但在加上影响概率的各种操作后（如主动向光源、折射方向采样）时，就比较难保持正确性。

我曾在应用多光源时采用了错误的办法，然后调了很久都调不出想要的效果…最后发现是概率在不经意间被我改变了，，，错误的方法可能导致收敛于一个错误的结果。

个人经验：想要快速判断自己的策略在期望上是否正确，可以简单地用最朴素的蒙特卡洛方法渲染一次（均匀采样，不加任何trick），只要渲染久一点，就能看到正确的效果是什么样的。

点光源

我们已经知道怎么在蒙特卡洛路径追踪中对面积光源进行采样，并且体现出“光源的照明效果与距离相关”这件事，对于点光源，如果我们之间加上特定方向的一根光线采样，点光源的距离不会影响照明，结果显然是不对的。

在mitsuba中，面积光源的强度单位是 Radiance，而点光源的单位是 Intensity，显然这不是随意命名的。这是辐射度量学的命名。点光源没有面积，无法用Radiance衡量表面亮度，因此用Intensity，相应的，在计算点光源贡献时，到达的 Radiance = Intensity / dis ^ 2

降噪

当前帧滤波

• 模糊操作：高斯滤波
• 保留一些高频的，边缘信息：双边滤波
  • 将颜色距离因素加入到滤波中去，如果两像素颜色差距较大，则减小贡献。
• 如何分辨边缘与噪声？额外信息：G-Buffer！

既然我们掌握了渲染的全过程，很容易得到一些如法线图、Albedo图，它们完全没有噪声。

类似双边滤波，我们可以将各种其他G-Buffer Feature添加到滤波中来加以指导，它们能非常有效地区分噪声和图像边缘，非常有效。

于是我们得到了联合双边滤波 Joint Bilateral Filtering

outlier/fire fly：蒙特卡洛方法容易产生一些过亮的点，也许要非常多sample才能将其平均下来；通常为了提速（并不物理正确），可以将其clamp掉。在滤波时，常将过高的颜色值clamp到 $[u-k\sigma,u+k\sigma]$ 上，同理Tempora中，也可以这么做。

TAA

https://zhuanlan.zhihu.com/p/425233743 这篇讲得很好

求一个 Motion Vector，即当前帧的像素，在上一帧的屏幕中的位置，以此混合历史像素。

混合时，可能有种种情况使得相同位置在当前帧与上一帧颜色不同（动态光源、动态物体、阴影变化等），可以利用GBuffer进行一些简单的判断来排除一些情况，但很难完全避免（例如阴影变化，就没什么很好办法能解决）。UE4的策略是利用当前帧像素的周围九个像素，计算出当前帧色彩的大致范围（可以计算颜色空间（通常转移到YCgCo下进行）的AABB来实现），混合历史帧时，clamp/clip在该范围外的信息。

另一种策略也是使用周围九宫格像素，但不直接计算包围盒，而是计算均值与方差，使用以均值为中心、若干个方差为宽度的AABB。

方差在降噪中是一个很重要的信息，降噪很多时候就是在噪声与overblur之间权衡，而方差可以指导我们动态地进行这种权衡，在噪声更严重的区域进行激进的降噪。

TODO

pixel reconstruction filter

Metropolis Light Transport

Photon Mapping

Radiosity Matrix