高质量补题记录集
本文最后更新于:2 年前
2022牛客第一场 J
一道不错的图论题
比较有价值的部分是图的合并,类似并查集,合并两点时可以使用其中一个点编号作为合并后的点集编号。
用启发式合并思想,让小集合向大集合合并,合并时将小集合上的连边转移到大集合上。
int n;
int fa[maxn], siz[maxn], cnt[maxn];
set<int> nt[maxn], fm[maxn];
int find(int x){
if(fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
void solve() {
cin >> n;
for(int i=1;i<=n;i++){
cnt[i] = 0;
nt[i].clear(), fm[i].clear();
fa[i] = i, siz[i] = 1;
}
for(int i=1;i<=n;i++){
int k; cin >> k;
cnt[i] = k;
for(int j=1;j<=k;j++){
int x; cin >> x;
nt[x].insert(i);
fm[i].insert(x);
}
}
queue<pair<int, int>> q; //存要合并的两个集合
for(int i=1;i<=n;i++){
if(cnt[i] == 1){
q.emplace(i, *fm[i].begin());
}
}
int ans = 1;
while(!q.empty()){
auto [x, y] = q.front();
q.pop();
//merge
x = find(x), y = find(y);
if(x == y) continue;
if(siz[x] > siz[y]) swap(x, y);
fa[x] = y;
siz[y] += siz[x];
ans = max(ans, siz[y]);
for(int v: nt[x]){
if(nt[y].count(v)){
cnt[v]--;
if(cnt[v] == 1) q.emplace(v, y);
nt[y].insert(v);
}
}
static int cas = 0;
cout << "Case #" << ++cas << ": " << ans << '\n';
}2022牛客第三场B
学到一个可删除堆的奇技淫巧,但这还不是关键
这里的最短路类似二分图和网络流中的“增广路”,路径代表的是一种转移方案,$a-b-c-d$ 这样的一条路径,实际上指将当前的人放到 $a$ 处,$a$ 中选取一个代价最小的人移到 $b$ 处…最后 $d$ 处多出一个人,最短路径即为将 $i$ 塞入的最小代价。
可以用一个set记录每个节点上已经有哪些人,记 $u,v$ 间的转移方案 ${dis,id}$,表示将 $id$ 这个人从 $u$ 转移到 $v$ 的代价为 $dis$,开 $K^2$ 个堆记录任意两点间的所有转移方案,在人员变动时维护。
template<typename T> struct heap{ //奇技淫巧:可删除堆 常数优秀
priority_queue<T, vector<T>, greater<T> > q1, q2;
void push(const T& x) {q1.push(x);}
void erase(const T& x) {q2.push(x);}
void release(){
while(!q1.empty() && !q2.empty() && q1.top() == q2.top()){
q1.pop();
q2.pop();
}
}
bool empty(){
release();
return q1.empty();
}
T top(){
release();
return q1.top();
}
};
int n, m;
heap<pair<ll, int>> tr[12][12]; //tr[x][y] 从x到y的所有可行路径,{dis, id}
set<int> nodes[12]; //存每个节点上所有的人
ll vol[maxn];
ll cost[maxn][12]; //基础花费:cost[x][k] x这个人匹配第k个城市的代价
ll move_dis(int u, int x, int y){ //转移代价:u这个人从x城切换到y城的代价
return cost[u][y] - cost[u][x];
}
pair<ll, int> min_dis(int x, int y){ //获取当前从x转移到y代价最小的路径
if(tr[x][y].empty()) return {INF, 0};
return tr[x][y].top();
}
void add(int k, int p){ //在k城添加一个人p,维护
nodes[k].insert(p);
for(int i=1;i<=m;i++){
if(i == k) continue;
tr[k][i].push({move_dis(p, k, i), p});
}
}
void remove(int k, int p){ //从k城移除一个人p,维护
nodes[k].erase(p);
for(int i=1;i<=m;i++){
if(i == k) continue;
tr[k][i].erase({move_dis(p, k, i), p});
}
}
void solve() {
cin >> n >> m;
for(int i=1;i<=m;i++) cin >> vol[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin >> cost[i][j];
}
}
ll ans = 0;
for(int i=1;i<=n;i++){
queue<int> q; //先跑最短路,即最小的将当前i塞进去的代价
vector<int> d(m+1);
vector<pair<int, int>> frm(m+1, {0, 0});
vector<bool> inq(m+1, true);
for(int j=1;j<=m;j++) q.push(j), d[j] = cost[i][j];
while(!q.empty()){
int u = q.front();
q.pop();
inq[u] = false;
for(int v=1;v<=m;v++){
if(v == u) continue;
auto [dis, id] = min_dis(u, v);
if(d[v] > d[u] + dis){
d[v] = d[u] + dis;
frm[v] = {u, id};
if(!inq[v]) q.push(v), inq[v] = true;
}
}
}
int ed = 0;
for(int j=1;j<=m;j++){
if(nodes[j].size() >= vol[j]) continue;
if(!ed || d[j] < d[ed]) ed = j;
}
assert(ed);
ans += d[ed]; //记录将i这个人塞进去的转移路径,沿着路径每个节点的状态,同时维护堆
while(true){
auto [fa, id] = frm[ed];
if(!fa){
add(ed, i);
break;
}
remove(fa, id);
add(ed, id);
ed = fa;
}
}
cout << ans << '\n';
}2022杭电第四场1002
边权有两种:距离和价值,要求一条距离最短前提下的价值最大的路。(距离可以为0)
因为距离为0,一条无距离有价值的路实际上相当于一条负权边,无法用传统dijkstra解决。
解法:先仅按照距离dij跑出到每个点的最短距离,得到最短路径图,在最短路径图上,tarjian缩点去除可能存在的环,变成一个DAG,再在DAG上跑最长路即可。
最短路径图即图上所有最短路径构成的图,可以从终点开始往前逆向跑,对于所有 $dis_v=dis_u+w$ 的路径加入最短路径图,也可以直接顺着跑,得到的点数会更多(包含了到所有点的最短路)。
DAG上的最长路可以按拓扑序更新(即一个点需要在前驱都遍历后更新),也可以直接spfa。
思路很简单,但是几层图换来换去代码属实调了很久,最后整出来这么一份非常结构化的代码,但还是很难直接拿去当图论模板..
struct Edge{
int t, w, val;
};
template<typename E>
class Graph{
public:
int n;
vector<vector<E>> vp;
Graph(int n): n(n), vp(n+1, vector<E>()){};
void addEdge(int x, const E &e){ vp[x].push_back(e);}
};
vector<ll> dijkstra(Graph<Edge> &g, int st){
using pii = pair<ll, int>;
vector<ll> dis(g.n+1, INF);
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, st}); dis[st] = 0;
while(!q.empty()){
pii uq = q.top();
ll ud = uq.first, u = uq.second;
q.pop();
if(ud > dis[u]) continue;
for(Edge &e: g.vp[u]){
int v = e.t;
if(dis[v] > dis[u] + e.w){
dis[v] = dis[u] + e.w;
q.push({dis[v], v});
}
}
}
return dis;
}
//获取最短路径图
Graph<pair<int, ll>> pathGraph(Graph<Edge> &g, int st){
auto dis = dijkstra(g, 1); //计算最短路
Graph<pair<int, ll>> res(g.n);
for(int i=1;i<=g.n;i++){
for(Edge &e: g.vp[i]){
int v = e.t;
if(dis[v] == dis[i] + e.w){
res.addEdge(i, {v, e.val});
}
}
}
cout << dis[g.n] << ' ';
return res;
}
namespace Connect{
int scc[maxn], stk[maxn], h, scn;
int dfn[maxn], low[maxn], dfc;
void tarjian(Graph<pair<int, ll>> &g,int p){
dfn[p] = low[p] = ++dfc;
stk[++h] = p;
for(auto &e: g.vp[p]){
int v = e.first;
if(!dfn[v]) {
tarjian(g, v);
low[p] = min(low[p], low[v]);
} else if(!scc[v]) {
low[p] = min(low[p], dfn[v]);
}
}
if(low[p] == dfn[p]){
++scn;
while(stk[h] != p) scc[stk[h--]] = scn;
scc[stk[h--]] = scn;
}
}
Graph<pair<int, ll>> getDag(Graph<pair<int, ll>> &g){
h = scn = dfc = 0;
for(int i=1;i<=g.n;i++) dfn[i] = scc[i] = 0;
for(int i=1;i<=g.n;i++) if(!scc[i]) tarjian(g, i);
Graph<pair<int, ll>> res(scn);
for(int i=1;i<=g.n;i++){
for(auto &e: g.vp[i]){
int v = e.first;
if(scc[i] != scc[v]){
res.addEdge(scc[i], {scc[v], e.second});
}
}
}
return res;
}
}
void solve(){
int n, m;
cin >> n >> m;
Graph<Edge> g(n);
for(int i=1;i<=m;i++){
int x, y, e, p;
cin >> x >> y >> e >> p;
g.addEdge(x, {y, e, p});
}
auto spg = pathGraph(g, 1);
auto dag = Connect::getDag(spg);
vector<ll> f(dag.n+1, 0), du(dag.n+1, 0);
for(int i=1;i<=dag.n;i++){
for(auto &e: dag.vp[i]){
du[e.first]++;
}
}
queue<int> q;
for(int i=1;i<=dag.n;i++) if(du[i] == 0) q.push(i);
while(!q.empty()){
int u = q.front();
q.pop();
for(auto &e: dag.vp[u]){
int v = e.first;
f[v] = max(f[v], f[u] + e.second);
if(--du[v] <= 0) q.push(v);
}
}
cout << f[Connect::scc[n]] << '\n';
}2022杭电第四场1005
矩阵+神奇双指针(对顶栈)
首先这题可以用矩阵维护一段区间的方案数,但矩阵并非一定可逆,故没法用前缀和搞。
比较容易想到的是线段树暴力维护矩阵区间乘,常数很大但是卡卡能过。
另有神奇的无需删除的双指针尺取(题解叫对顶栈):
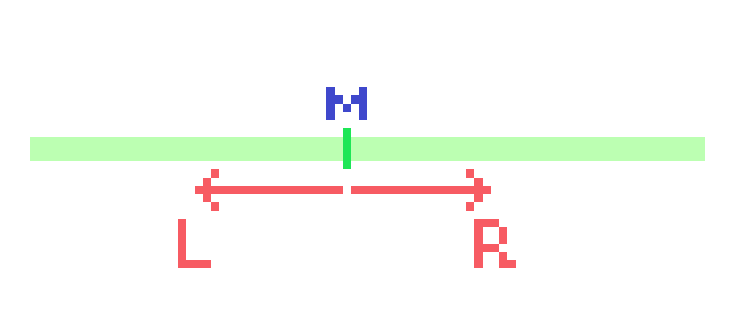
如图所示,双指针 $l,r$ 即为两个栈顶,右指针移动时将新元素加入右栈中;左指针移动时将栈顶元素弹出,接触到中间点时,将右栈的所有元素一一弹出并加入左栈,将右端点作为新的中点。
左栈中加入元素时记录该元素到中点的后缀和,这样在左栈弹出后,仍可以得知左栈的总和,和右栈和相加得到区间和(此题中为积)。
如此便可以 $O(n)$ 地做不带删除的尺取了!
int lim;
struct matrix{
static const int N = 21, M = 21;
ll a[N][M];
matrix(int x = 0){ //单位矩阵
memset(a, 0, sizeof(a));
for(int i=1;i<=N;i++) a[i][i] = x;
}
inline matrix operator*(const matrix& y) const{
matrix r = 0;
for (int i = 0; i < N; ++i)
for (int k = 0; k < M; ++k) {
ll t = a[i][k];
for (int j = 0; j < M; ++j){
r.a[i][j] += t * y.a[k][j];
if(r.a[i][j] > lim) r.a[i][j] = lim + 1;
}
}
return r;
}
};
matrix a[maxn], s[maxn];
void solve(){
int n, m;
cin >> n >> m >> lim;
for(int i=1;i<=n;i++){
int l; cin >> l;
a[i] = 1;
for(int j=1;j<=l;j++){
int x, y; cin >> x >> y;
a[i].a[x][y] = 1;
}
}
matrix cur(1);
auto check = [&](int l, int r){
ll ans = 0;
for(int i=1;i<=m;i++){
ans += s[l].a[1][i] * cur.a[i][m];
if(ans > lim) return false;
}
return true;
};
int ans = 0, mid = 0;
for(int l=0, r=1; r<=n; r++){
cur = cur * a[r];
while(l == 0 || !check(l, r)){
l++;
if(l > mid){
s[r] = a[r];
for(int i=r-1;i>mid;i--) s[i] = a[i] * s[i+1];
mid = r;
cur = 1;
}
}
ans = max(ans, r - l + 1);
}
cout << ans << '\n';
}2022杭电第八场1002
大力数据结构维护题。
从左往右推,设 $f_i$ 为前 $i$ 个位置划分好的方案数,接下来要转移到 $i+1$。
维护两个单调栈,一个递增一个递减,对于递增单调栈中相邻两个位置 $x,y$,可以知道 $(x,y]$ 这段作为起始位置时,最小值都为 $a_y$。那么就可以知道:这段区间中的所有奇数/偶数位置都能满足最小值条件。
对于最大值条件也是同理,可以用两个线段树分别维护奇偶位置上的tag(满足条件数),同时满足两个条件的位置即可进行转移。
线段树中,维护每个区间的最大满足条件的数量(tag),和具有最大条件数量的位置的 $f_i$ 之和。对线段树的操作包括单点添加新的dp值,区间tag加1和减1(在单调栈中元素被pop时减)。
因为我们的操作能保证合理(只对具有tag1区间的减tag1,tag2一样),所以不需要记录区间具有两种条件的哪一种,只需要记录数量即可。
int n, a[maxn];
ll f[maxn];
struct segTree {
function<int(int)> fp; //自带离散映射的线段树
ll sum[maxn << 2], mx[maxn << 2];
int add[maxn << 2];
void build(int p, int l, int r) {
add[p] = sum[p] = mx[p] = 0;
if(l == r) return;
int mid = (l + r) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
}
void push_up(int p) {
sum[p] = 0, mx[p] = max(mx[p * 2], mx[p * 2 + 1]);
if(mx[p] == mx[p * 2]) (sum[p] += sum[p * 2]) %= mode;
if(mx[p] == mx[p * 2 + 1]) (sum[p] += sum[p * 2 + 1]) %= mode;
}
void push_add(int p, int d) {
mx[p] += d;
add[p] += d;
}
void push_down(int p) {
if(add[p]) {
push_add(p * 2, add[p]);
push_add(p * 2 + 1, add[p]);
add[p] = 0;
}
}
void addvalue(int p, int l, int r, int pos, ll val) {
if(l == r) {
(sum[p] += val) %= mode;
return;
}
push_down(p);
int mid = (l + r) / 2;
if(pos <= fp(mid)) addvalue(p * 2, l, mid, pos, val);
else addvalue(p * 2 + 1, mid + 1, r, pos, val);
push_up(p);
}
void modify(int p, int l, int r, int L, int R, int d) {
if(fp(l) > R || L > fp(r)) return;
if(L <= fp(l) && fp(r) <= R) {
push_add(p, d);
return;
}
push_down(p);
int mid = (l + r) / 2;
modify(p * 2, l, mid, L, R, d);
modify(p * 2 + 1, mid + 1, r, L, R, d);
push_up(p);
}
ll queryTot() {
if(mx[1] == 2) return sum[1];
else return 0;
}
}st[2];
int stk[2][maxn], h[2];
void solve() {
cin >> n;
for(int i = 1;i <= n;i++) cin >> a[i];
st[0].fp = [](int x) { return 2 * x;};
st[1].fp = [](int x) { return 2 * x - 1;};
int hn = (n + 1) / 2;
st[0].build(1, 1, hn);
st[1].build(1, 1, hn);
h[0] = h[1] = 0;
stk[1][++h[1]] = stk[0][++h[0]] = 0;
f[0] = 1;
for(int i = 1;i <= n;i++) {
st[i & 1].addvalue(1, 1, hn, i, f[i - 1]);
while(h[0] > 1 && a[stk[0][h[0]]] > a[i]) {
int f = stk[0][h[0]] & 1;
st[f ^ 1].modify(1, 1, hn, stk[0][h[0] - 1] + 1, stk[0][h[0]], -1);
h[0]--;
}
st[(i & 1) ^ 1].modify(1, 1, hn, stk[0][h[0]] + 1, i, 1);
stk[0][++h[0]] = i;
while(h[1] > 1 && a[stk[1][h[1]]] < a[i]) {
int f = stk[1][h[1]] & 1;
st[f].modify(1, 1, hn, stk[1][h[1] - 1] + 1, stk[1][h[1]], -1);
h[1]--;
}
st[i & 1].modify(1, 1, hn, stk[1][h[1]] + 1, i, 1);
stk[1][++h[1]] = i;
f[i] = (st[0].queryTot() + st[1].queryTot()) % mode;
}
cout << f[n] << '\n';
}2022杭电第八场1009
感觉挺妙的一个线段树上概率处理+线段树合并
对于每个点 $u$,它连向子树的边中一定只存在一条有颜色。
考虑 $u$ 的这个子树中的每个操作,将它们按照时间排序,一个操作能为 $u$ 的连边作出贡献,当且仅当这个操作成功,且之后的操作都失败。
把操作按时间放到线段树上,区间维护 $sxp$ 表示区间内所有操作的 $1-p$ 乘积(全失败的概率),和 $sum$ 表示 $c_i\times p_i\times\prod_{j>i}(1-p_{j})$ 的总和。即期望贡献。
这两个信息很好push_up。
那么对于每个点 $u$,将其子树的线段树合并起来之后取 $sum$ 即可得到它连儿子边的总贡献,注意还要考虑 $u$ 这个点本身的操作会将边权清空,计算sum时可以先将 $u$ 本身的操作的 $c_i$ 视为0加入线段树,处理贡献后再将 $c_i$ 改回来。
struct segTree {
ll sum[maxn << 5], sxp[maxn << 5];
int ls[maxn << 5], rs[maxn << 5];
int tcnt = 0;
int newnode() {
++tcnt;
sum[tcnt] = 0;
sxp[tcnt] = 1;
ls[tcnt] = rs[tcnt] = 0;
return tcnt;
}
void push_up(int p) {
sum[p] = (sum[ls[p]] * sxp[rs[p]] % mode + sum[rs[p]]) % mode;
sxp[p] = sxp[ls[p]] * sxp[rs[p]] % mode;
}
int merge(int x, int y, int l, int r) {
if(!x) return y;
if(!y) return x;
assert(l != r);
int mid = (l + r) / 2;
ls[x] = merge(ls[x], ls[y], l, mid);
rs[x] = merge(rs[x], rs[y], mid + 1, r);
push_up(x);
return x;
}
int modify(int p, int l, int r, int pos, ll pi, ll ci) {
if(!p) p = newnode();
if(l == r) {
sxp[p] = (1ll - pi + mode) % mode;
sum[p] = pi * ci % mode;
return p;
}
int mid = (l + r) / 2;
if(pos <= mid) ls[p] = modify(ls[p], l, mid, pos, pi, ci);
else rs[p] = modify(rs[p], mid + 1, r, pos, pi, ci);
push_up(p);
return p;
}
}st;
int n, m;
vector<int> vp[maxn];
vector<array<int, 3>> opt[maxn];
ll ans = 0;
int dfs(int p) { //返回子树的线段树根节点
int rt = st.newnode();
for(auto tup: opt[p]) {
int id = tup[0], pi = tup[1];
st.modify(rt, 1, m, id, pi, 0);
}
for(int v : vp[p]) rt = st.merge(rt, dfs(v), 1, m);
(ans += st.sum[rt]) %= mode;
for(auto tup : opt[p]) {
int id = tup[0], pi = tup[1], ci = tup[2];
st.modify(rt, 1, m, id, pi, ci);
}
return rt;
}
void solve() {
st.tcnt = -1;
st.newnode(); //初始化0点
ans = 0;
cin >> n >> m;
for(int i = 1;i <= n;i++) {
vp[i].clear();
opt[i].clear();
}
for(int i = 2;i <= n;i++) {
int fa; cin >> fa;
vp[fa].push_back(i);
}
for(int i = 1;i <= m;i++) {
int x, c, p;
cin >> x >> c >> p;
opt[x].push_back({i, p, c});
}
dfs(1);
cout << ans << '\n';
}2022杭电第九场1001
比较难想到是构造题
需要不包含任何等差数列,一个可以切入的思考点是:等差数列要么全是奇数/偶数,要么在奇偶之间来回切换
如果把奇数放到一边,偶数放到另一边,那么必然不存在跨两边的等差数列,就可以分治求解了。
奇数部分可以集体-1,偶数部分可以集体除2,都不影响等差数列的存在性。
int n, a[maxn];
void cdq(int l, int r) {
if(l + 1 >= r) return;
int m = l;
for(int i = l;i <= r;i++) if(a[i] & 1) swap(a[m++], a[i]);
for(int i = l;i < m;i++) a[i]--;
cdq(l, m - 1);
for(int i = m;i <= r;i++) a[i] /= 2;
cdq(m, r);
for(int i = l;i < m;i++) a[i]++;
for(int i = m;i <= r;i++) a[i] *= 2;
}
void solve() {
cin >> n;
for(int i = 1;i <= n;i++) cin >> a[i];
sort(a + 1, a + n + 1);
for(int i = 3;i <= n;i++) if(a[i] == a[i - 1] && a[i] == a[i - 2]) {
cout << "NO\n";
return;
}
cdq(1, n);
cout << "YES\n";
for(int i = 1;i <= n;i++) cout << a[i] << " \n"[i == n];
}2022杭电第十场1008
对于静态森林,可以求出各个树的直径,将其他小直径的中点和最大直径的中点相连,答案易得。
所以问题转化为动态维护树上直径,操作只有连边
我们可以单开一个并查集记录每个树的直径以及直径两端点,合并两树时,只需考虑四个端点的两两组合,合并后的直径一定在它们当中。
使用LCT可以快速求出任意两点间距离,且支持森林连边操作。
struct LCT {
int ch[maxn][2], fa[maxn], siz[maxn], swp[maxn];
inline int dir(int p) { return ch[fa[p]][1] == p; }
inline void push_up(int p) { siz[p] = 1 + siz[ch[p][0]] + siz[ch[p][1]]; }//sum[p] = sum[ch[p][0]] ^ sum[ch[p][1]] ^ val[p]; }
inline bool isroot(int p) { return fa[p] == 0 || (ch[fa[p]][0] != p && ch[fa[p]][1] != p); } //是否为splay的根(不是原树的根!)
inline void push_swap(int p) {
if(!p) return;
swap(ch[p][0], ch[p][1]), swp[p] ^= 1;
// push_down(p);//调试用 立即下放所有懒标记
}
inline void push_down(int p) {
if(swp[p]) {
swp[p] = 0;
push_swap(ch[p][0]);
push_swap(ch[p][1]);
}
}
void rotate(int p) {//出bug了必须首先来查rotate 注意变化前后顺序的问题 太麻了
if(fa[p] == 0) return;
int f = fa[p], ff = fa[f];
int d = dir(p), s = ch[p][d ^ 1];
if(!isroot(f)) ch[ff][dir(f)] = p;//与普通splay不同之处:如果父亲节点已经是根节点,一定不能让ff认儿子
fa[s] = f;
fa[p] = ff; ch[p][d ^ 1] = f;
fa[f] = p; ch[f][d] = s;
push_up(f);//最后一个节点的push_up在splay那
}
void push_all(int p) {
if(!isroot(p)) push_all(fa[p]);
push_down(p);
}
void splay(int p) {//将p转到其所在splay(实链节点集合)的根节点
push_all(p);//从顶向下push_down
while(!isroot(p)) {
if(!isroot(fa[p])) rotate(dir(p) == dir(fa[p]) ? fa[p] : p);
rotate(p);//双旋,不管旋了父还是子,第二次旋转都要跟上,不然会假
}
push_up(p);
}
void access(int p) {//打通p所在真实树的根节点到p的路径
int lst = 0;
while(p) {
splay(p);
ch[p][1] = lst;
push_up(p);
lst = p;
p = fa[p];
}
}
void makeroot(int p) {//p变为其所在真实树中的根节点(同时也是splay根)
access(p);
splay(p);
push_swap(p);
}
int findroot(int p) {//查找所在真实树的根节点,注意这个也会改变p所在splay结构
access(p);
splay(p);
while(ch[p][0]) push_down(p), p = ch[p][0];
return p;
}
void split(int x, int y) {//将x,y之间的路径剖出来作为splay,然后x作为原树根,y作为splay根
makeroot(x);
access(y);
splay(y);
}
void link(int x, int y) {//连边(虚边)
makeroot(x);
if(x != findroot(y)) fa[x] = y;//注意,连虚边一定要让所在splay的根节点的fa连出去,这里x已经是splay根节点了而y不一定
}
void cut(int x, int y) {//删边
if(findroot(x) != findroot(y)) return;
split(x, y);//记牢此时x为原树根,y为splay根,原树根仅仅是深度最小的节点,完全可以有fa
if(fa[x] != y || ch[x][1]) return;//要x,y之间有连边,就要它们在splay的中序遍历上相邻
ch[y][0] = fa[x] = 0;
push_up(y);
}
int dist(int x, int y) {
split(x, y);
return siz[y];
}
void init(int n) {
for(int i = 0;i <= n;i++) ch[i][0] = ch[i][1] = fa[i] = swp[i] = 0;
}
}lct;
int a[maxn], f[maxn];
struct diameter {
int x, y, d;
bool operator <(const diameter& t)const {
return d < t.d;
}
}d[maxn];
int find(int x) {
if(x == f[x]) return x;
return f[x] = find(f[x]);
}
int cnt[maxn];
void solve() {
int n, m;
cin >> n >> m;
lct.init(n);
cnt[0] = 0;
for(int i = 1;i <= n;i++) {
f[i] = i;
lct.siz[i] = 1;
d[i] = {i, i, 0};
cnt[i] = 0;
cnt[0]++;
}
int mxd = 0;
for(int i = 1;i <= m;i++) {
int x, y; cin >> x >> y;
int fx = find(x), fy = find(y);
cnt[d[fx].d]--;
cnt[d[fy].d]--;
lct.link(x, y);
diameter tmp = max(d[fx], d[fy]);
tmp = max(tmp, {d[fx].x, d[fy].x, lct.dist(d[fx].x, d[fy].x) - 1});
tmp = max(tmp, {d[fx].x, d[fy].y, lct.dist(d[fx].x, d[fy].y) - 1});
tmp = max(tmp, {d[fx].y, d[fy].x, lct.dist(d[fx].y, d[fy].x) - 1});
tmp = max(tmp, {d[fx].y, d[fy].y, lct.dist(d[fx].y, d[fy].y) - 1});
f[fx] = fy;
d[fy] = tmp;
cnt[tmp.d]++;
mxd = max(mxd, tmp.d);
// for(auto x : alld) cout << x << ' ';
// cout << '\n';
int mx[4], h = 0;
for(int i = 1;h < 3 && i <= cnt[mxd];i++) mx[++h] = mxd;
if(mxd > 0) for(int i = 1;h < 3 && i <= cnt[mxd - 1];i++) mx[++h] = mxd - 1;
if(mxd > 1) for(int i = 1;h < 3 && i <= cnt[mxd - 2];i++) mx[++h] = mxd - 2;
int ans = mx[1];
if(h > 1) ans = max(ans, (mx[1] + 1) / 2 + 1 + (mx[2] + 1) / 2);
if(h > 2) ans = max(ans, (mx[2] + 1) / 2 + 2 + (mx[3] + 1) / 2);
cout << ans << '\n';
}
}COMPFEST 14 J. Journey
如果只有一个起点,答案即所有边权x2再减去树上的最长路径(直径)
现在可以取第二个起点,那么答案(要减去的部分)有两种情况:
- 树上两条有单个点相交的路径
- 树上两条不相交的路径,再加上两路径之间的最大边x2
对于第一种情况,考虑枚举交点,然后走四条链出去,这个比较好维护
第二种情况,枚举中间边,然后需要知道以这条边作为分割,上下两棵树的直径。
要维护这两个东西比较麻烦,具体如下:
ll dia[maxn]; // p这个子树的直径
ll dup[maxn]; // 除去p子树的直径
ll dp[maxn][4]; // p向下最大的四条链
ll dp2[maxn][2];// p儿子中最大的两个直径
ll up[maxn]; // p向上走的最长链首先一遍 dfs 求出 dp, dp2, dia
然后再 dfs 第二遍,这一遍从上向下转移
设当前跑到边 $u\rightarrow v$,边权 $w$
up[v] 可以由 up[u] + w,以及 u子树中除了v之外的最长链 + w 转移来
dup[v] 可以由 dup[u] 以及 u子树中除了v之外的最大直径 和 u连出的链中除了v之外的最大两条链之和 转移来
想到了这些就会发现题目可做了,然后就是分类讨论的事了(
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 1e6 + 100;
const int mode = 1e9 + 7;
vector<pair<int, ll>> vp[maxn];
ll dia[maxn]; // p子树的直径
ll dup[maxn]; // 除去p子树的直径
ll dp[maxn][4]; // p向下最大的四条链
ll dp2[maxn][2];// p儿子中最大的两个直径
ll up[maxn]; // 向上最长链
void add1to(int p, ll val){
for(int i = 0;i < 4;i++) {
if(dp[p][i] < val) swap(val, dp[p][i]);
}
}
void add2to(int p, ll val) {
for(int i = 0;i < 2;i++) {
if(dp2[p][i] < val) swap(val, dp2[p][i]);
}
}
void dfs(int p, int fa) {
dia[p] = 0;
for(auto [v, w] : vp[p]) {
if(v != fa) {
dfs(v, p);
add1to(p, dp[v][0] + w);
add2to(p, dia[v]);
dia[p] = max(dia[p], dia[v]);
}
}
dia[p] = max(dia[p], dp[p][0] + dp[p][1]);
}
void dfs2(int p, int fa, ll& res) {
ll tmp;
add1to(p, up[p]);
for(auto [v, w] : vp[p]) {
if(v != fa) {
up[v] = w + dp[p][dp[p][0] == dp[v][0] + w ? 1 : 0];
ll mx1 = dp2[p][dp2[p][0] == dia[v] ? 1 : 0];
ll mx2;
if(dp[p][0] == dp[v][0] + w) mx2 = dp[p][1] + dp[p][2];
else if(dp[p][1] == dp[v][0] + w) mx2 = dp[p][0] + dp[p][2];
else mx2 = dp[p][0] + dp[p][1];
dup[v] = max({dup[p], mx1, mx2});
res = max(res, dia[v] + dup[v] + 2 * w);
dfs2(v, p, res);
}
}
}
void solve() {
int n;
cin >> n;
ll ans = 0;
for(int i = 1;i < n;i++) {
int u, v, w; cin >> u >> v >> w;
vp[u].emplace_back(v, w);
vp[v].emplace_back(u, w);
ans += w * 2;
}
dfs(1, 0);
ll res = 0;
dfs2(1, 0, res);
for(int i = 1;i <= n;i++) {
if(vp[i].size() < 4) continue;
res = max(res, dp[i][0] + dp[i][1] + dp[i][2] + dp[i][3]);
}
cout << ans - res << '\n';
}2022 ICPC 网赛2 H
首先分别考虑贡献,因为这题中一个方案的贡献由所有 $u,v$ 间的路径长度( $u,v$ 之间没有其他选中点)组成,故去考虑每一条路径 的贡献。
一条路径计入答案,当且仅当其两端点 $u,v$ 都选中,且路径中其他点都不被选中(仅计算被直接选择时的贡献,作为子路径时不考虑,这样能做到不重复不遗漏),然后我们再去考虑这个路径会被计算多少次。
此时其他点可选可不选,对于任意一点 $i$,它对这个路径产生贡献的次数都为 $2^{n-d-2}$,那么这条路径的总贡献为:$d(n-d+3)2^{n-d-2}$
有了这个式子,只需要枚举图中所有的路径计算和即可,但这显然不现实。
考虑换根dp,对于每个点记录其向上走和向下走的所有路径贡献和,如何转移?
注意到每条路径的式子形式类似 $xy2^y$,对于许多这样的式子和,要进行全体 x+1 等类似操作并维护是很容易的,只需要维护 $x2^y,y2^y,2^y$ 和作为辅助即可。
同理进行 y-1 等操作也不难,剩下的就是一个标准的换根dp了。
ll qpow(ll x, ll p) {
if(p < 0) return qpow(qpow(x, -p), mode - 2);
ll r = 1;
while(p > 0) {
if(p & 1) r = r * x % mode;
x = x * x % mode;
p /= 2;
}
return r;
}
ll iv2 = qpow(2, mode - 2);
struct node {
ll xxy, xy, yy, y;
node() : xxy(0), xy(0), yy(0), y(0) {};
node(ll a, ll b) {
y = qpow(2, b);
yy = b * y % mode;
xy = a * y % mode;
xxy = b * xy % mode;
}
node operator +(const node& t) {
node r = *this;
(r.xxy += t.xxy) %= mode;
(r.xy += t.xy) %= mode;
(r.yy += t.yy) %= mode;
(r.y += t.y) %= mode;
return r;
}
node operator -(const node& t) {
node r = *this;
(r.xxy -= t.xxy) %= mode;
(r.xy -= t.xy) %= mode;
(r.yy -= t.yy) %= mode;
(r.y -= t.y) %= mode;
return r;
}
node add1() {
node r(0, 0);
r.xxy = (xxy + yy - xy - y + 2 * mode) % mode * iv2 % mode;
r.yy = (yy - y + mode) * iv2 % mode;
r.xy = (xy + y) * iv2 % mode;
r.y = y * iv2 % mode;
return r;
}
};
int n;
vector<int> vp[maxn];
node dw[maxn], up[maxn];
void dfs1(int p, int fa) {
dw[p] = node(0, n + 3);
for(int v : vp[p]) {
if(v != fa) {
dfs1(v, p);
dw[p] = dw[p] + dw[v].add1();
}
}
}
void dfs2(int p, int fa) {
for(int v : vp[p]) {
if(v != fa) {
up[v] = (up[p] + dw[p] - dw[v].add1()).add1();
dfs2(v, p);
}
}
}
void solve() {
cin >> n;
for(int i = 1;i < n;i++) {
int x, y; cin >> x >> y;
vp[x].push_back(y);
vp[y].push_back(x);
}
dfs1(1, 0);
dfs2(1, 0);
ll ans = 0;
for(int i = 1;i <= n;i++) ans = (ans + (up[i] + dw[i] - node(0, n + 3)).xxy) % mode;
cout << ans * qpow(64, mode - 2) % mode << '\n';
}2022 CCPC 威海 K
题意:要求寻找区间 $[l, r](0<l\le r)$ 的个数,满足给出的 $n$ 个条件,条件形式如下:
- 1 $k$ $x$:可以在 $[l,r]$ 中找出 $k$ 个不同数,使得他们的和为 $x$
- 2 $k$ $x$:无法在 $[l,r]$ 中找出 $k$ 个不同数,使得他们的和为 $x$
首先注意到一点:对于任意区间 $[l,r]$,从中取 $k$ 个数的值域是连续的,最小值为 $\frac{(l+l+k-1)\times l}{2}$,最大值同理(式子不写了)
考虑第一种条件,我们可以找到这样一个区间: $[L,L+k-1]$ 总和为 $x$,或者 $[L,L+k]$,前 $k$ 个数和小于 $x$ 且后 $k$ 个数和大于 $x$。
条件一转化为:$[l,r]$ 必须包括这个区间,可以合并所有条件一得到 $l$ 的最大值和 $r$ 的最小值。
同理,条件二转化为 $[l,r]$ 必须不包括这个区间,然而这个东西在线段上比较难处理,可以在 $lOr$ 平面上考虑。
画个图发现就是求个矩形面积并,可以扫描线或者单调栈处理。
void solve() {
int n; cin >> n;
ll L = 2e9, R = 0;
vector<pii> ban;
for(int i = 1;i <= n;i++) {
int opt, k, x;
cin >> opt >> k >> x;
ll l = 1, r = 2e9;
while(l < r) {
ll mid = (l + r) / 2;
ll val = (mid + mid + k - 1) * k / 2;
if(val >= x) r = mid;
else l = mid + 1;
}
r = l + k - 1;
ll val = (l + l + k - 1) * k / 2;
if(val != x) l--;
if(opt == 1) {
L = min(L, l);
R = max(R, r);
} else {
if(l == 0) continue;
ban.emplace_back(l, r);
}
}
if(L == 0) {
cout << "0\n";
return;
}
if(ban.empty()) {
cout << "-1\n";
return;
}
for(auto& [x, y] : ban) {
if(x > L) x = L;
if(y < R) y = R;
}
sort(ban.begin(), ban.end(), [&](pii& a, pii& b) { return a.second < b.second;});
stack<pii> stk;
for(auto& [x, y] : ban) {
if(stk.empty() || x > stk.top().first) {
stk.emplace(x, y);
}
}
if(stk.top().first < L) {
cout << "-1\n";
return;
}
ll ans = 0;
ll lst = stk.top().second;
stk.pop();
while(!stk.empty()) {
auto [x, y] = stk.top();
stk.pop();
ans += (lst - y) * (L - x);
lst = y;
}
ans += (lst - R) * L;
cout << ans << '\n';
}2022 CCPC 威海 F
题意:给出一个有向图,每个点有颜色 $c_i$ 和费用 $w_i$,走到一个未打标记的点时,需花费 $w_i$ 并打标记,随后你可以选择任意个颜色不同的节点 $j$,回收上面的标记并返还 $w_j$ 的费用。
问:对于每一对起点终点,初始需要多少钱才能抵达。 $n \le 300$
显然当我们走到一个点时,会选择回收所有不同颜色的节点的费用,
那么对于一条路径,把它拆分为若干颜色段,走到每一段时都会回收前一段的费用,那么这段路径的代价就是MAX(每一段的费用和+下一段第一个点的费用,最后一段的费用)
就变成了一个瓶颈路的问题。
具体做法:把原图划分为若干个同颜色的连通块,在每个连通块内部floyd求出两两间最短路,然后枚举块内的起点($s$)和终点($t$),再枚举终点向块外连的边($t\rightarrow j$),在新图上建一条 $s\rightarrow j$ 的边。
在新图上枚举起点,朴素prim跑最小瓶颈路($n^2$)
这样就将 “每一段的费用和+下一段第一个点的费用” 考虑完了,还需要考虑最后一段的费用,这个不能直接在块内连边,因为我们要求最小瓶颈路,边权不能“合成”。(这个词用的比较抽象,自行理解一下)
只需要在最后输出前,用块内其他点+块内距离松弛一次即可,同样因为边不能“合成”,松弛后的结果不能更新到最短路中,而应当直接输出。
ll dis[303][303];
int col[303], w[303];
bool vis[303];
vector<int> vp1[303];
ll dis2[303][303];
void dfs(int p, vector<int>& ls) { //染色
vis[p] = true;
ls.push_back(p);
for(int v : vp1[p]) {
if(!vis[v] && col[v] == col[p]) {
dfs(v, ls);
}
}
}
void solve() {
int n, m;
cin >> n >> m;
fill(dis[0], dis[0] + 303 * 303, 1e18);
fill(dis2[0], dis2[0] + 303 * 303, 1e18);
fill(vis, vis + n + 1, false);
for(int i = 1;i <= n;i++) {
vp1[i].clear();
}
for(int i = 1;i <= n;i++) cin >> col[i];
for(int i = 1;i <= n;i++) cin >> w[i], dis[i][i] = w[i];
for(int i = 1;i <= m;i++) {
int x, y; cin >> x >> y;
vp1[x].push_back(y);
vp1[y].push_back(x);
dis[x][y] = dis[y][x] = w[x] + w[y];
}
for(int i = 1;i <= n;i++) {
if(!vis[i]) {
vector<int> ls;
dfs(i, ls);
for(int k : ls) {
for(int i : ls) {
for(int j : ls) {
if(dis[i][k] + dis[k][j] - w[k] < dis[i][j]) {
dis[i][j] = dis[j][i] = dis[i][k] + dis[k][j] - w[k];
}
}
}
}
for(int i : ls) {
for(int j : ls) {
for(int v : vp1[j]) {
if(col[j] != col[v]) {
dis2[i][v] = min(dis2[i][v], dis[i][j] + w[v]);
}
}
}
}
}
}
vector ans(n + 1, vector<ll>(n + 1, 1e18));
for(int i = 1;i <= n;i++) {
ans[i][i] = w[i];
fill(vis, vis + n + 1, false);
for(int cc = 1;cc <= n;cc++) { //prim
int p = 0; ans[i][0] = 1e18;
for(int j = 1;j <= n;j++) {
if(!vis[j] && ans[i][j] < ans[i][p]) p = j;
}
vis[p] = true;
for(int v = 1;v <= n;v++) {
ans[i][v] = min(ans[i][v], max(ans[i][p], dis2[p][v]));
}
}
}
for(int i = 1;i <= n;i++) {
for(int j = 1;j <= n;j++) {
ll opt = ans[i][j];
// 最后一步可以使用dis
for(int k = 1;k <= n;k++) {
opt = min(opt, max(ans[i][k], dis[k][j]));
}
if(i == j) opt = 0;
cout << opt << " \n"[j == n];
}
}
}