新生赛题解之chiking的俄罗斯方块

XX的俄罗斯方块

时间限制：1000ms 空间限制：256M

题目背景:

XX沉迷一款叫俄罗斯方块的游戏，但这个游戏对他来说实在太难了，于是它决定玩无敌版

无敌版俄罗斯方块中，有一个宽4格，高度无限的网格图，游戏流程如下：

1. 初始时网格图为空

2. 一个由方块组成的砖块（只有1x4和2x2两种）出现在网格图内很高的地方，XX可以对它进行任意次操作：

   1. 将这个方块整体左移一格（不能被已有的方块阻挡或超出边界）
   2. 将这个方块整体右移一格（不能被已有的方块阻挡或超出边界）

3. 砖块块每隔一段时间就会整体下落一格（当然由于XX的手速非常快，它可以在下落的间隙中进行无数次平移），当因被阻挡或即将超出下边界而无法下落时，它就会固定，紧接着出现下一个砖块

4. 方块固定后，如果有一整行的四格方块都填满，这一行将被消除，XX得到1分；如果一次同时消除了多行，第二行将能得到2分，第三行就是3分，以此类推。

   所以一次性消除4行就能获得一共10分！

注意：砖块不可分割，不可旋转，所有1x4的砖块均竖直，且保证1x4的方块仅出现偶数次

下面这种插入方式也是允许的：

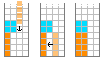
题目描述：

XX现在正在打一局无敌版的俄罗斯方块，他知道接下来出现的 n 个砖块的种类，你能帮他算一算他最高能获得多少分吗？

输入格式：

输入有两行

第一行一个正整数 n，表示接下来有 n 个砖块 (1<= n <= 10^6)

第二行 n 个正整数，依次表示接下来出现的砖块种类，0表示 2x2 的砖块，1表示 1x4 的砖块

输出格式：

输出一个正整数，为XX能获得的最大分数

样例输入：

4
0 1 1 0

样例输出：

6

样例解释：

按下面这种方式堆放：

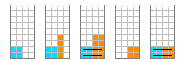
第三个插入时连消了两行，获得1+2分

第五个插入时连消了两行，获得1+2分

一共6分，不存在比这得分更多的方案

---

题解：

先说结论：

用任何方式算出最大四连消的次数即可，其余尽可能多地三连消，最后可能剩余一个 $2\times2$ 或者 $2\times4$，可以发现一点：只要存在正方形的砖块，最后就不可能剩下 $2\times4$ 的情况。

---

首先可以看出，只有2连消和4连消两种消法，分别对应3分和10分；

从贪心的角度来讲，我们需要尽可能多4连消；随便定一个数字 $k$，考虑怎么去判断能否进行 $k$ 次4连消：

• $k$ 至多为1的数量的一半；
• 先在第四列堆 $k$ 根1x4，在前两列尽可能堆高，最后 $k$ 根长条都插入第三列，这样能尽可能保证4连消；
• 在这种策略下，如果在第三列每根1*4插入时，前两列高度都 $\ge4$，则能够进行 $k$ 次4连消，否则一定不能；

所以进行 $k$ 次4连消的条件就是：对于任意倒数第 $b$ 个1 ($b\le k$)，都满足到这里为止，前面可用的1和0在前两列能够堆的高度 $\ge$ $(k-b+1) \times4$，所谓“可用的0和1”就是指所有的0和去掉放在第四列的 $k$ 个和第三列的 $k-b+1$ 个1；

即对于任意倒数第 $b$ 个1（$b\le k$），假设它在第 $i$ 位，满足 $(cnt1[i]-k-(k-b+1))/2\times4 + cnt0[i]\times2\ge(k-b+1)\times4$

其中 $cnt0[i]$，$cnt1[i]$ 分别为前 $i$ 个块中0，1的数量；（式中除号为整除）

有了这个式子，最大的 $k$ 就不难算了：初始将 $k$ 设为 $cnt1[n]/2$，我们从后往前枚举，每枚举到一个1时就依据上式判断，不断减小 $k$ 直到上式成立，这样就得到了最大的 $k$。

---

有必要解释一下：$x$ 个 1可以在前两列堆出 $x/2\times4$ 的高度：（式中除号为整除）

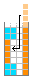
当插入一根1x4时，直接放在第一列，接下来如果是方块则正常放置不影响，下一根1x4用这种插入的方式补在第二列即可，因为直到最后 $k$ 个1之前第三列都是空的，这种方式一定行的通。

---

一二列堆的多余部分要尽可能2连消，这个比较简单，堆的高度超出 $k\times4$ 后左右来回放就行了，总得分就是 $k\times4+(n-k)/2\times3$，最后可能会剩余1个2x2，这个没有办法消除；（式中除号为整除）

最后也有可能不得不剩下两根1x4，这种情况当且仅当全场都是1的时候才成立，否则一定能通过改变一个0的位置消掉（感性理解即可，想要严格证明可以私聊我，不太好讲）

因为 $k$ 是最大的4连消次数，在此情况下也最多只会浪费两个方块，减少4连消次数损失的10收益远大于可能获得的3收益，所以这就是得分最大的方案。

int n, a[maxn];
int cnt0[maxn], cnt1[maxn];

int main() {
    cin >> n;
    for(int i=1;i<=n;i++) cin >> a[i];
    for(int i=1;i<=n;i++){
        cnt0[i] = cnt0[i-1];
        cnt1[i] = cnt1[i-1];
        if(a[i] == 0) cnt0[i]++;
        else cnt1[i]++;
    }
    int k = cnt1[n] / 2;
    int brk = 0;
    for(int i=n;i>=1;i--){
        if(a[i] == 1){
            brk++;
            while(k >= brk && (cnt1[i]-(k+k-brk+1))/2*4 + cnt0[i]*2 < (k-brk+1)*4) k--;
        }
    }
    if(cnt0[n]) cout << k*10+(n-k*4)/2*3 << '\n';
    else cout << n/4*10 << '\n';

    return 0;
}

PS：由于这题最终答案偏差不大，其他贪心方式也有机会通过（

来自老老会长的ac代码：

void solve() {
    int n;
    cin >> n;
    vector<int> data(n), lPos;
    vector<bool> flag(n, true);
    queue<int> oPos;
    for (int i = 0; i < n; ++i) cin >> data[i];
    int res = 0, tot2 = 0;
    // 2*2 + 2*2 + 1*4 + 1*4
    for (int i = 0; i < n; ++i) {
        if (data[i] == 0) {
            oPos.push(i);
            tot2++;
        } else {
            if ((int) oPos.size() >= 2 && (int) lPos.size() >= 1) {
                flag[oPos.front()] = false;
                oPos.pop();
                flag[oPos.front()] = false;
                oPos.pop();
                flag[lPos.back()] = false;
                flag[i] = false;
                lPos.pop_back();
                res += 10;
            } else {
                lPos.push_back(i);
            }
        }
    }

    int cnt1 = (int) lPos.size();
    int cnt2 = (int) oPos.size();

    // 1*4 + 1*4 + 1*4 + 1*4
    int tmp = cnt1 / 4;
    res += tmp * 10;
    cnt1 -= tmp * 4;


    // 1*4 + 1*4 + 2*2 + 2*2
    if (cnt1 == 2 && cnt2 >= 2) {
        res += 6;
        cnt2 -= 2;
        cnt1 -= 2;
    }

    // 2*2 + 2*2
    res += 3 * (cnt2 / 2);

    if (cnt1 == 2 && (cnt2 == 1 || tot2 >= 2)) {
        res += 3;
    }

    cout << res << endl;
}